Abstract
It is a stylized fact that the Italian farmers do not benefit of casual structure along value chain. Conversely, retailers could advantage of any positive shock price changes occurred in the wholesale supply chain. We investigate the presence of shock price vertical contagion in the Italian hog market, describing the dependence structure along the supply chain and assessing the degree of extreme value dependence. The approach followed is non linear and copula-based, applied on weekly data of hog price changes referred to Italian farm, wholesale and retail branch chain, over the period 1994-2015. In particular, the objective of the analysis consists in to obtain a measure of the relationship between extreme events of returns, estimating the tail dependence coefficients of copula functions involved in the analysis. The empirical findings highlight the asymmetry of price transmission along the hog Italian supply chain, more relevant for wholesale–retail pair.
DOI: 10.30682/nm1901a
Fabian Capitanio*, Felice Adinolfi**, Barry K. Goodwin***, Giorgia Rivieccio****
* Department of Agricultural Economics and Policy, University of Naples Federico II, Italy.
** Department of Veterinary Medical Sciences DIMEVET, University of Bologna, Italy.
**** University of North Carolina, US.
**** University of Naples Parthenope, Italy.
Corresponding author: fabian.capitanio@unina.it
Cite this Item: Capitanio F., Adinolfi F., Goodwin B. K., Rivieccio G., A copula-based approach to investigate vertical shock price transmission in the italian hog market, New Medit, 18 (1): pp. 3-14, http://dx.doi.org/10.30682/nm1901a
1. Introduction
Agro-food price asymmetry contagion, under extreme market conditions, is an important yardstick for measuring market inefficiencies. On one hand, this is of relevance from micro-perspective as large and unexpected price movements strongly affect agricultural households’ welfare. On the other hand, market distortions are often cited as a ground for government intervention. In this sense, the problem of market volatility is also high on the agenda from macro-perspective.
In well-functioning markets, price shocks are equally transmitted at all market levels, from retailers to producers passing along the wholesale level; in trade terms, would be crucial to evaluate the dependence structure among global food grain markets and South Eastern Mediterranean Countries (SEMC). In this context, it would be relevant to know dependence structure because it could be a risk management tool for speculators and a better forecasting tool for implement public support to risk management and food security. The efficiency of a food supply chain is, therefore, crucial to maintain a sustainable distribution of value added and of benefits among the stakeholders (Emmanouilides and Fousekis, 2014)
Volatility of agricultural commodity international price has a greater impact on developing countries and on the poorer, because it creates major import bill uncertainty.
Currently 16% of the world population use the opportunities of international trade to cover their demand for agricultural products.
In the SEMC, food security is strongly interrelated with several key economic and political issues. Many of these countries are becoming increasingly import-dependent, particularly on cereals, which are the essential raw material for human and animal food and feed. The SEMC are responsible for 1/3 of world cereals imports, whereas they account for only 5% of the world population.
The exposure of SEMC countries to world food price volatility is firstly linked to their high dependence on the external market. The World Bank (2012) has calculated the ratios of net imports to domestic consumption, as indicative of the dependency on foreign imports to satisfy domestic food demand . The results show that dependence on food imports in general is high across SEMC countries.
In this scenario, several researches have been carried out in order to consider the possible price asymmetry dependence structure, conditioned to direction or magnitude of changes, such as Boyd and Brorsen (1988), which tested, in both cases, for asymmetry in price adjustments in the pork marketing channel, verifying that wholesaler price changes are affected, symmetrically, by price changes occurred at farmer level, and Goodwin and Harper (2000), that revealed important asymmetries in the U.S. pork sector with a threshold co-integration model, and Ben-Kaabia and Gil (2007) that analyzed a three-regime Threshold Autoregressive Model to verify price asymmetry transmission in Spanish lamb sector. Other models are based on non-stationary feature of time series data, by means of co-integration techniques, see e.g. the regime-switching model of Serra and Goodwin (2003) or the asymmetric long run price linkage of Gervais (2011) and price transmission elasticity of Abbassi et al. (2012).
Anyway, all these models do not take into account, simultaneously, some aspects, such as to model separately the marginal and joint dependence structure of variables in a non-linear and flexible way, to measure the interdependence in presence of extreme market events, in terms of tail dependence measures, and to consider the conditional volatility of time series.
More recently works study the asymmetry in the world of copulas. The copula tool is quite popular in finance and risk management area since the late 1990s (see, for instance, Cherubini et al., 2004; Patton, 2006), but only recently are applied in agro-food economics.
Copulas offer an alternative and flexible way to analyze price co-movements, particularly during extreme market events. A copula function allows to specify, separately, the joint dependence structure from the marginal behavior of time series, enabling a conditional dependence evaluation between extreme events by means of tail dependence coefficients, as measure of the relationship in the tails of the joint distribution. In addition, in order to consider the conditional volatility of each time series, a copula-GARCH approach can be used, allowing to describe time-varying variance of univariate returns.
The latest agro-food economics literature is rich enough of empirical contributes aimed to explore market integration in the copula context. Reboredo (2012) examined co-movement between international food and oil prices; Serra and Gill (2012) analyzed the relationship among biodiesel, diesel and crude oil prices in Spain; Emmanouilides and Fousekis (2014) investigated vertical price dependence in the U.S. beef supply chain, verifying the presence of asymmetry influences in the market, especially for the pair wholesale–retail which is only of positive type; finally, Panagiotou and Stavrakoudis (2015), studying the price dependence structure between different pork cuts in the U.S. industry at retail level, did not find evidence of asymmetry in the price co-movements. In this perspective, analyzing the U.S. hog/pork market, Qiu and Goodwin (2013) explored asymmetric vertical transmission of price changes along the supply chain under extreme market conditions, by means of tail dependence measures based on a copula-GARCH model, applied also in a time-varying framework. Their results show the evidence of symmetric shock price change transmission along farm – wholesale and wholesale – retail pairwise; conversely, the farm– retail return pair is characterized by an asymmetric relationship in the tail of the joint distribution, higher for the upper than for the lower case. This last feature means that positive extreme returns in one marketing channel, e.g. for the farmer, are connected to positive extreme returns in the other one, for the retailer, and vice versa.
Then, in order to measure the asymmetry of shock price transmission along the Italian hog supply chain, starting from the idea of Qiu and Goodwin (2013) and defining the joint co-movement of farm, wholesale and retail price changes, a copula-based approach has been applied, which enables to estimate the dependence structure in presence of extreme values assumed by returns.
Moreover, since 2008 the European Commission has stressed that the experience of the 2007/2008 price peaks has shown that magnitude and asymmetry recorded in the price adjustment process represent serious concerns about the functioning of the European agro-food supply (EC, 2008). The same report underlines how the empirical evidence in this regard is, however, contrasting, highlighting even very different conclusions depending on the markets and the countries investigated. Same conclusions for the specific sector of the hog supply chain, for which the Commission found, however, some significant trends, such as the slowness with which in many countries price changes move from upstream to downstream, symptomatic of the fact that only a limited part of the changes in consumer prices is generated by changes recorded in the primary phase of the supply chain, and the presence of imperfections in the competitive structure of the supply chains.
In Italy the question is of particular importance for the value generated by the supply chain. One of the most advocated options is to promote, within the framework of the discipline of inter-professional organization, long-term contracts shared by an important part of the operators in the supply chain and based on indexation mechanisms connected, at least in part, to feed prices, which represents about 40% of the average costs borne by Italian pig producers.
In this context, the aim of this work is threefold. First of all, to the best of our knowledge, we contribute to the literature as the primary attempt in agro-food Italian market in the copula tool framework, then, we describe the relationship among extreme values along Italian hog supply chain also in terms of trivariate copula tail dependence measures, both in the upper and lower case and, finally, we define the policy implications of the analysis results.
The paper is structured as follows: a short theoretical backgrounds are given in Section 2, focusing, in particular, on statistical properties of copula functions, of tail dependence coefficients and of non-parametric tail dependence measures; more details are provided in Appendix 1. The Section 3 provides empirical results of the analysis of joint tail co-movements along the Italian hog supply chain. Some concluding remarks are reported in Section 4.
2. Theoretical Framework
2.1. Copula function properties
A copula function is an n-variate distribution function defined on the unit cube [0, 1]n, with uniformly distributed margins, with the following properties:
– he range of copula C(u1, . . . , un) is the unit interval [0, 1];
– (u1, . . . , un) = 0 if any ui = 0 for i = 1, . . . , n;
– (1, . . . , 1, ui, 1, . . . , 1) = ui for all ui ϵ [0, 1];
The copula-based pillar is the Sklar’s theorem (Sklar, 1959), which justifies the role of copula as dependence function, shows that, for continuous multivariate distributions, the univariate margins can be separated from the dependence structure which is completely captured by a copula function.
Theorem 1: Let H(·) be a joint distribution function of continuous random variables xi (for i = 1,…, n) with marginal distribution functions Fi(·), then, there exists a copula function C, such that:
H(x1, . . . , xn) = C(F1(x1), . . . , Fn(xn))
where Fi(·)=P(Xi ≤ xi)=ui (for i = 1, . . . , n) and every ui = (u1, . . . , un)T is uniform in [0, 1]n.
If Fi(·) is continuous, then the copula C is unique; otherwise, C is uniquely determined on [RanF1(x1), . . . ,RanFn(xn)]. Conversely, if C is a copula and Fi(·) is a distribution function, then the function H defined above is a joint distribution function with margin Fi(·).
3. Empirical analysis
3.1. Data and modeling procedure
We have analysed the price co-movements in the hog Italian market, verifying the dependence structure of hog weekly data prices, from January 1994 to December 2014, concerning the farm, wholesale and retail distribution channels.
The analysis of prices reveals that a crisis in the hog market begun in the 1998 continued throughout the 1999, in all three chains. Besides, a more recent shock in the farm market occurred in the 2008, as shown in the Figure 1, as result of high levels of raw material costs employed in the breeding and of energy resources.
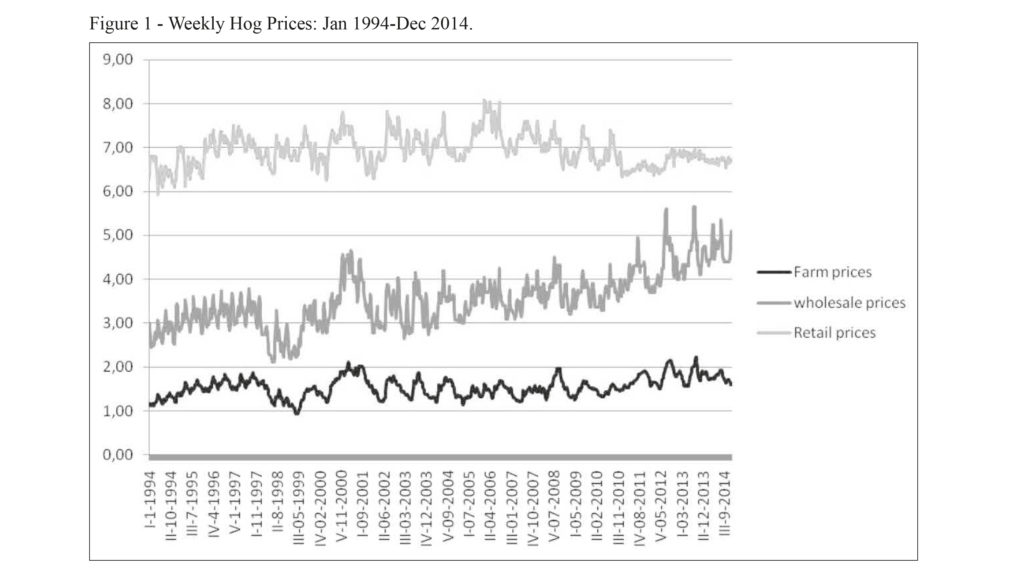
In all three series is not present any trend, as showed by the results of Augmented Dickey-Fuller (ADF) test (Dickey and Fuller, 1979) applied to farm, wholesale and retail price time series.
Moreover, we intend to study the supply chain co-movements of weekly returns. Therefore, in the first, we have obtained log-returns, calculating the natural logarithm of ratios between the price at time t and the same price at time t-1, for each branch chain. Then, an ARMA-GARCH model has been applied to taking into account the presence of a conditional serial dependence of returns, both in mean and in variance framework. After estimating marginal behaviour of each time series of returns, we investigated the presence of a conditional cross-section dependence (as suggested in Qui and Goodwin, 2013), applying a cross-equation model to the standardized residual pair-wise obtained from the estimated ARMA-GARCH structure. Afterwards, we transform the standardized residuals of cross-equation model into uniform margins, input argument of copula functions. Concluding, a copula function has been employed to join the uniform margins into a multivariate distribution. This method, called Inference For Margins (IFM) method, allows to specify separately, in a simple (instead of the full maximum likelihood, more computationally complex) and flexible way (also in non linear and asymmetric framework), the dependence structure of returns, by means of the maximum likelihood estimation method for the parameters involved at each step of the procedure.
Finally, in order to measure the conditional dependence between extreme events occurred along the pork supply chain, tail dependence coefficients are estimated.
We derived, besides, a trivariate copula function in order to estimate the upper and lower tail dependence coefficients among the three branch chains. Starting from the standardize skew-t residuals of an ARMA-GARCH model before and, then, on the residuals of the conditional cross-equation model (VAR) with skew-t innovations, we applied the uniform transformation to obtain the trivariate copula margins. Then, a copula model is selected from the main families, such as Elliptical and Archimedean. In this case, the method could consist in a non-linear VAR (Vector AutoRegressive) model (see, e.g. Bianchi et al., 2010) with three variables, applying a copula function on VAR skew-elliptical distributed residuals. Tail dependence coefficients for the multivariate t-copula are obtained according to Joe (2014).
3.2. Results
The analysis of branch chain returns highlights a more high volatility of wholesale returns (see Table 1), while the farm and retail returns are quite stable over the time, reporting very low fluctuations in the considered period.
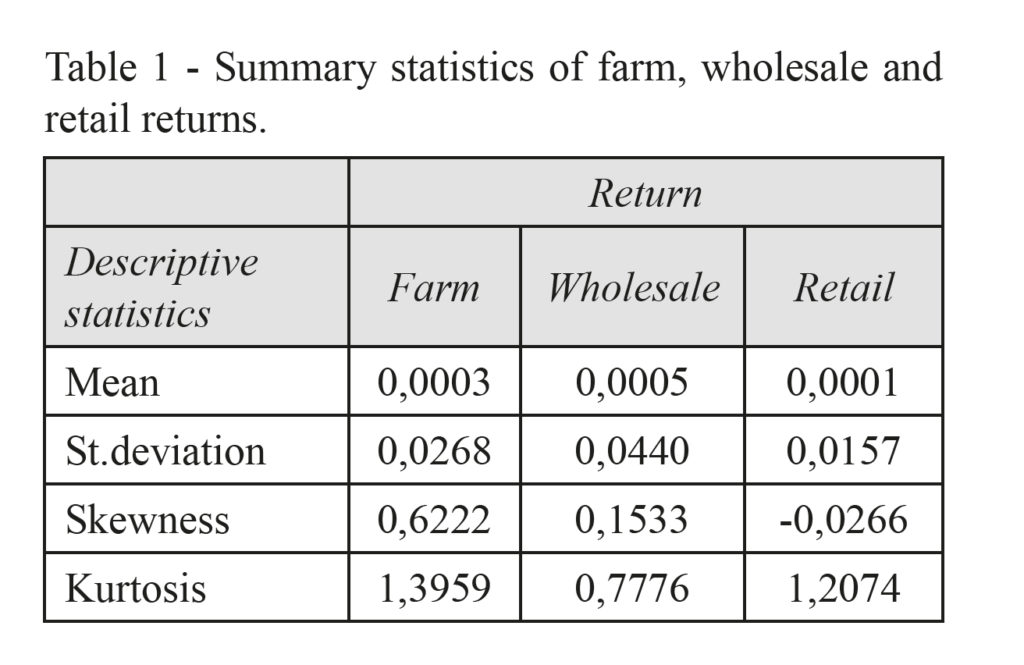
In addition, calculating the non parametric tail dependence measures at same time lag t (Table 2), we note a significant upper tail dependence between farm and retail returns and a symmetric non-zero tail dependence between farm and wholesale price changes. This implies that, in the same week, positive extreme values of farm prices changes are linked to positive extreme values of retail returns, and vice versa; but negative shocks of a variable does not affect the other one. For the pair farm-wholesale, we observe a significant joint tail co-movement, both in the upper and lower case.
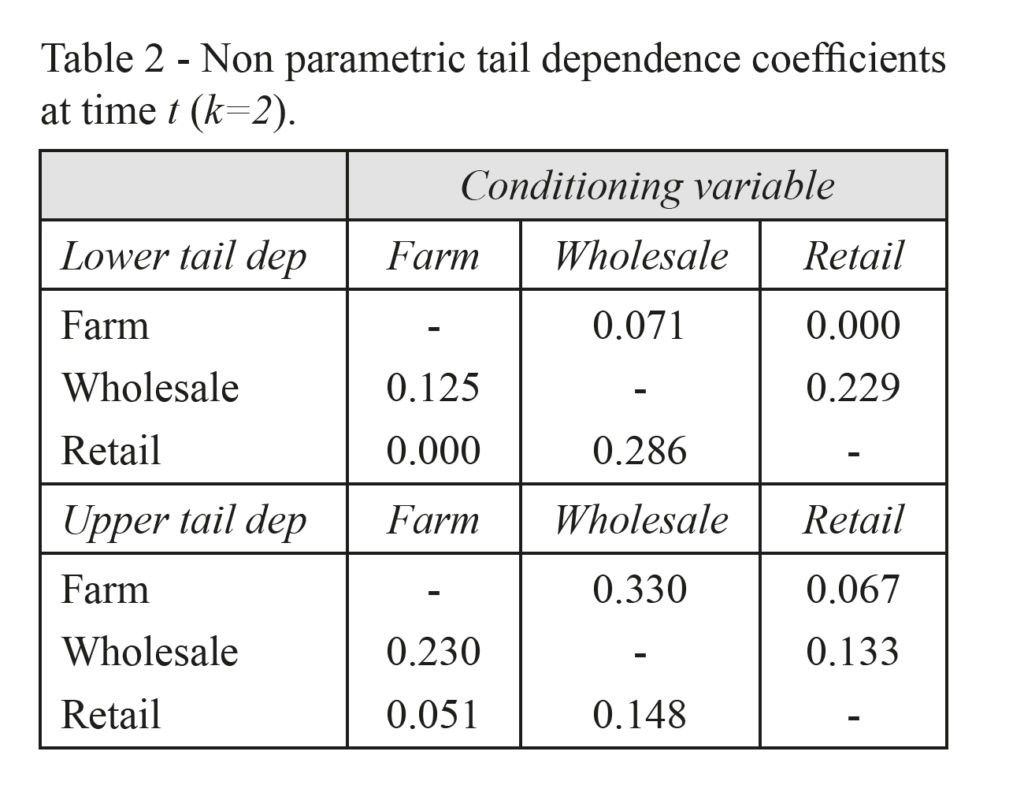
Conversely, the non parametric tail dependence measures, if calculated at different time lag, between t and t-1 (or two consecutive weeks) on each asset pair-wise (Table 3), exhibit the absence of tail dependence, in the lower case, between retail/wholesale and farm price changes, as conditioning variable. This could mean an absence of effects of farm extreme negative returns over retail/wholesale price changes at different lags. If farm chain has a lower return in a week, other prices do not change the next week. In the upper case, the impact is the same. Then, positive extreme events occurred in one week for farm, do not impact on the other variables in the following week. The impulse response function, typical of Vector Autoregressive models, could show this asymmetrical behaviour.
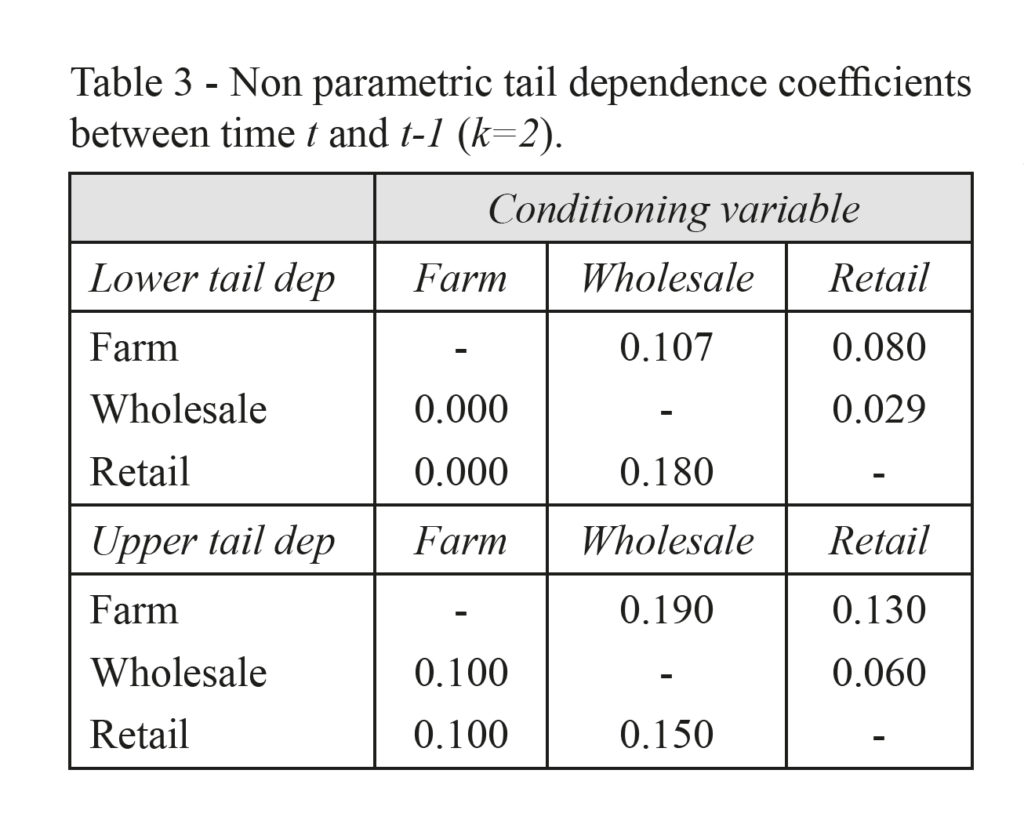
On the other side, the non parametric tail dependence coefficients displayed between retail and wholesale is symmetrical in both quadrant of the joint distribution, justifying the application of a symmetrical tail dependence copula, like the Student’s- t copula function. In particular, the non parametric tail dependence values suggest that the extreme returns at farm level do not affect extreme wholesale and retail price changes, if considered at different period of observation, and this future could suggest the use of a null tail dependence copula, like the Frank copula. But the values of non parametric tail dependence coefficients calculated for the same week (t) for each return pair lead to apply an upper tail dependence copula, e.g. the Gumbel copula.
For this reason, we have analysed all well-known copula functions, which belong to Elliptical and Archimedean families, characterize by all tail dependence structures.
Table 4 are presents the parameter values obtained applying the ARMA-GARCH model, with innovations skew-t distributed, to the three univariate returns and by the cross-equation effect model employed on each return pair. The significant lag order is 1 for wholesale/retail with respect to farm price changes (at t-1, the previous week) and for farm/retail with respect to wholesale returns (at t-1); on the contrary, farm/wholesale – retail pair-wise do not show any significant lag order; in this last case, there is not evidence of relationship over the time among retail and the remaining two market chains.
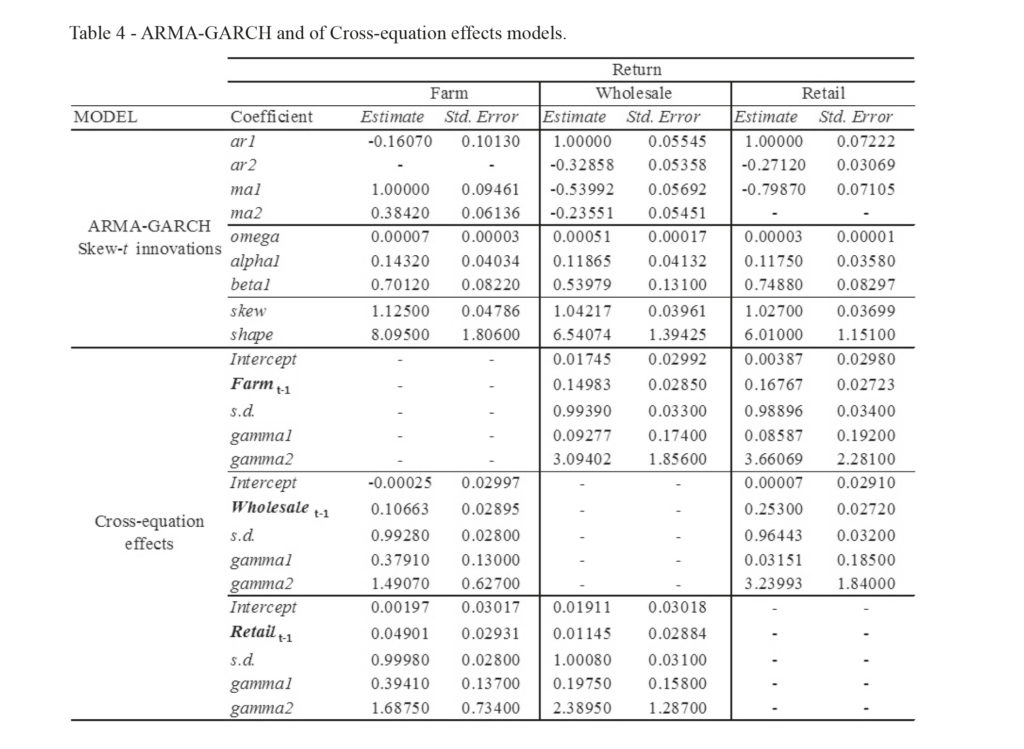
Below, Table 5 reports the fitting values of some main copulas involved in the analysis. We have estimated all possible copula pairs, choosing the copula with the best fit to the data, according to the minimum value assumed by Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC).
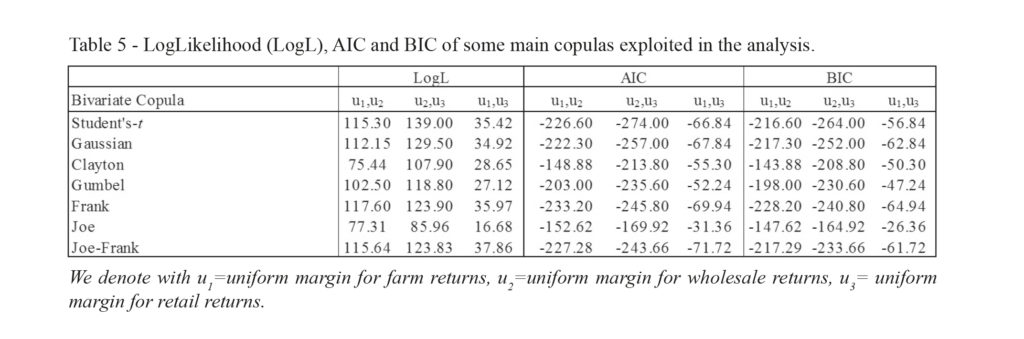
The best fit copula model for the first pair of assets, denoted as u1 and u2, respectively farm and wholesale returns, is the Frank copula, that implies a null tail dependence, both for the upper and lower coefficients; this means that extreme values of a variable have no influence on the other ones. Therefore, the upper tail dependence, exhibited between farm and wholesale price changes at the same week, becomes not significant when calculated after using conditional mean and variance model for returns. As a matter of fact, the Gumbel copula exhibits the best fit to the data when the IFM method is applied in absence of a conditional model for the price changes, such as the ARMA-GARCH model and the conditional serial dependence equations. In addition, not considering the cross-equation effects, the copulas are identical to the copulas obtained taking into account the cross-section dependence between variables. This means that only the univariate conditional dependence in mean and variance has really influence on dependence structure of returns.
Conversely, the copula that better represents the dependence structure between wholesale and retail price changes is the Student’s-t copula, which is characterized by symmetric non-null tail dependence coefficients (λL = λU = 0.065). This suggests a weak relationship in the tail of joint distribution, such that positive (negative) shock for wholesale (retail) returns are followed by positive (negative) shock for retail (wholesale) returns at the same time.
Also for the last return pair, farm and retail, the tail dependence coefficient is null, because the choice of copula lies on two copulas (AIC value suggests the selection of Joe-Frank copula, while the BIC value indicates the Frank copula, both characterized by null tail dependence coefficients). The symmetric extreme price changes co-movements are annulled by the conditional structure of returns, in the univariate and bivariate framework. This feature leads to conclude that joint co-movements under extreme market conditions are weak or null.
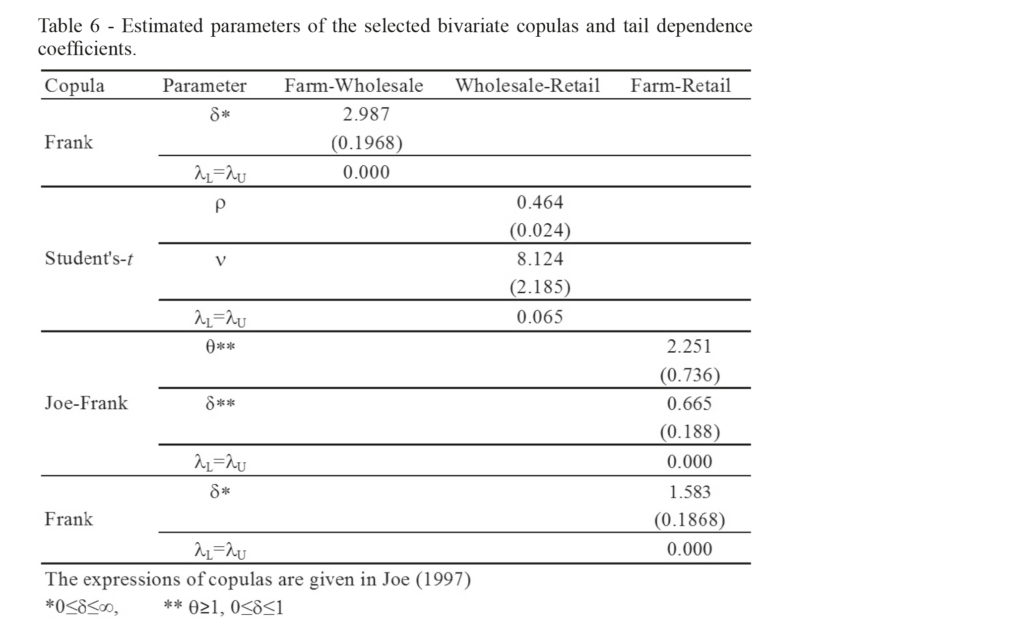
Further, we want to verify the presence of a conditional dependence in the tails of the trivariate joint distribution, in order to assess the degree of this relationship considering the whole dependence structure of the pork supply chain. To this end, we estimate some copulas as reported in Table 7, according to the procedure described in Section 3.1.
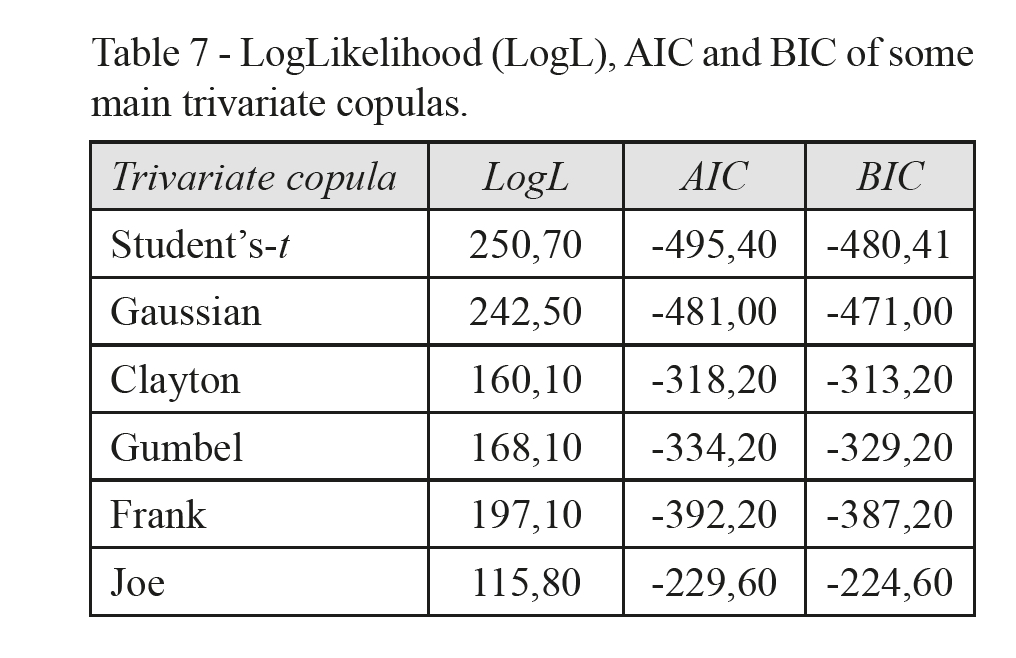
The results show the best fit of the t-Copula with symmetrical, not null, tail dependence. Tail dependence coefficients reported at the end of Table 8, measure the relationship between extreme values at the same lag t. As shown in Table 8, the tail dependence coefficients are quite low, underlying the same conclusions pointed out in the the bivariate case and by the non parametric tail dependence, higher for wholesale-retail pair and close to zero for those remaining.
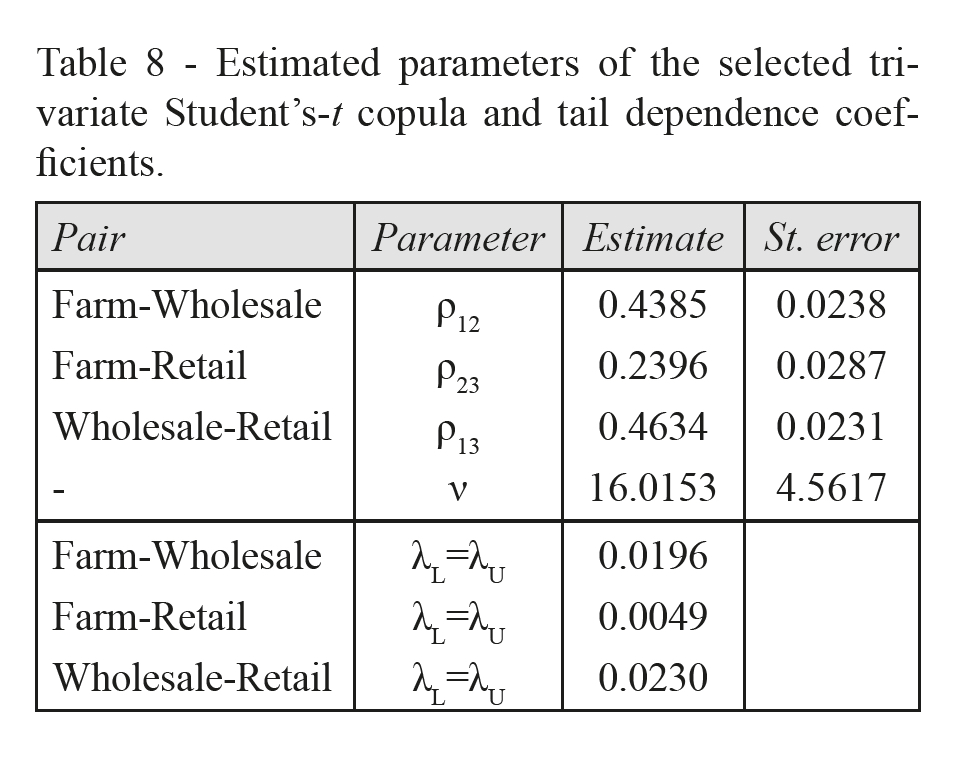
This price adjustment asymmetry in favour of retail-wholesale channels reflects the weakness of the producer that fails to adjust prices under positive extreme market conditions. In the same way, in case of extreme negative conditions at farm level, retail/wholesale prices will not reproduce the same remarkable reduction.
4. Conclusion
It is important to distinguish between analyses of evolution of margins over time and price transmission as these topics are closely related but are not identical. Conclusions about price transmission that are drawn from the evolution of marketing margins over time, but that do not incorporate other information such as the changes in the costs of other inputs, may be misleading.
This paper focused to an analysis of vertical price transmission.
The adjustment to price shocks along the chain from producer to wholesale and to retail levels, and vice versa, is an important characteristic of the functioning of markets. As such, the process of price transmission through the supply chain has long attracted the attention of agricultural economists, as well as policy makers. Recently, the subject of price transmission has been increasingly linked to the discussion about benefits from agricultural reform e.g. Common Agricultural Policy post 2013. That is, a common concern of policy makers relates to the assertion that, due to imperfect price transmission (perceived to be caused by market power and oligopolistic behavior), a price reduction at the farm level is only slowly, and possibly not fully, transmitted through the supply chain. In contrast, price increases at the farm level are thought to be passed more quickly on to the final consumer.
An implication of this asymmetry in price transmission, if it exists, is that an analysis of trade liberalization likely over-estimates the benefits to consumers in countries that have gone through policy reform, because the reduction in farm prices might not be immediately or fully transmitted to final consumers.
As a result, there would be smaller positive effects on consumer welfare and a possible increase in rents for the firms in the downstream sector. Thus, it is important to understand the processes related to pass-though of price changes as price transmission assumptions along the supply chain play an important role in determining the size and distribution of welfare effects of trade policy reform.
In our analysis we estimated the tail co-movements in the joint distribution along hog supply chain in Italy, following the approach proposed in Qiu and Goodwin, 2013.
It turned out that tail price co-movement for farm-wholesale pair is null and it is well described with a Frank copula, characterized by zero tail dependence, such as for the pair farm-retail, whose dependence structure is defined by a Joe Frank copula; conversely, the relationship among wholesale-retail price changes is symmetrical and rather weak, but not null, and it is represented by a Student’s-t copula, with identical non zero tail dependence coefficients.
These results underline an asymmetrical shock price vertical contagion, showing a better price adjustments along the wholesale–retail chain.
This conclusion emphasized what we above introduced on the relevance to catch and possibly to foresee the price transmission movement along value chain and/or among different countries.
The value chain in the hog supply chain is effectively integrated and the policy decisions at one point will cause ripple effect on the other linkages. Hence, the policies should take into account the effect of impact on the entire value chain as to enable the hog producers capture the benefits of value addition.
Moreover, this new methodological approach seems very promising to analyze price transmission in agricultural commodity trade that, for SEMC would represents a big challenges to tackle food security.
References
Abbassi A., Tamini L.D. and Gervais J.P., 2012. Do Inventories Have an Impact on Price Transmission? Evidence From the Canadian Chicken Industry. Agribusiness, 28(2): 173-186.
Ben-Kaabia M. and Gil J., 2007. Asymmetric price transmission in the Spanish lamb sector. European Review of Agricultural Economics, 34: 53-80.
Bianchi C., Carta A., Fantazzini D., De Giuli M.E. and Maggi M.A., 2010. A copula-VAR-X approach for industrial production modelling and forecasting. Applied Economics, 42: 3267-3277.
Boyd M.S. and Brorsen B.W., 1988. Price asymmetry in the us pork marketing channel. North Cent J Agric Econ., 10(1): 103-109.
Cherubini U., Luciano E. and Vecchiato W., 2004. Copula Methods in Finance. Chichester: John Wiley & Sons.
De Luca G., Rivieccio G., 2009. Archimedean copulae for risk measurement. Journal of Applied Statistics, 36(8): 907-924.
De Luca G., Rivieccio G., 2012. Multivariate tail dependence coefficients for Archimedean Copulae. In: Di Ciaccio A. et al. (eds.), Advanced Statistical Methods for the Analysis of Large Data-Sets, Studies in Theoretical and Applied Statistics, Springer, DOI: 10.1007/978-3-642-21037-2 26.
Dickey D.A. and Fuller W.A., 1979. Distribution of the Estimators for Autoregressive Time Series With a Unit Root. Journal of the American Statistical Association, 74: 427-431.
Emmanouilides C.J. and Fousekis P., 2014. Vertical price dependence structures: copula-based evidence from the beef supply chain in the USA. European Review of Agricultural Economics, 1-21, DOI: 10.1093/erae/jbu006.
European Commission, EC, 2008. High prices on agricultural commodity markets: situation and prospects.
Gervais J.P., 2011. Disentangling nonlinearities in the long- and the short-run price relationships: an application to the US hog/pork supply chain. Applied Economics, 43: 1497-1510.
Goodwin B.K. and Harper D.C., 2000. Price transmission, threshold behavior, and asymmetric adjustments in the U.S. pork sector. Journal of Agriculture and Applied Economics, 32: 543-553.
Joe H., 1997. Multivariate Models and Dependence Concepts. New York: Chapman & Hall/CRC.
Joe H., 2014. Dependence Modeling with Copulas. New York: Chapman & Hall/CRC.
Nelsen R., 2006. An Introduction to Copulas. New York: Springer.
Panagiotou D. and Stavrakoudis A., 2015. Price asymmetry between different pork cuts in the USA: a copula approach. Agricultural and Food Economics 3: 6, DOI: 10.1186/s40100-015-0029-2.
Patton A., 2006. Modelling asymmetric exchange rate dependence. Int. Econ. Rev. 47: 527-556.
Qiu F. and Goodwin B.K., 2013. Measuring Asymmetric Price Transmission in the U.S. Hog/Pork Markets: A Dynamic Conditional Copula Approach, Applied Commodity Price Analysis, Forecasting, And Market Risk Management.
Reboredo J.C., 2012. Do food and oil prices co-move? Energy Policy, 49: 456-467.
Serra T. and Gil J.M., 2012. Biodiesel as a motor fuel price stabilization mechanism. Energy Policy, 50: 689-698.
Sklar A., 1959. Fonctions de repartition an dimensions et leurs marges. Publ. Inst. Statist. Univ. Paris, 8: 229-231.











