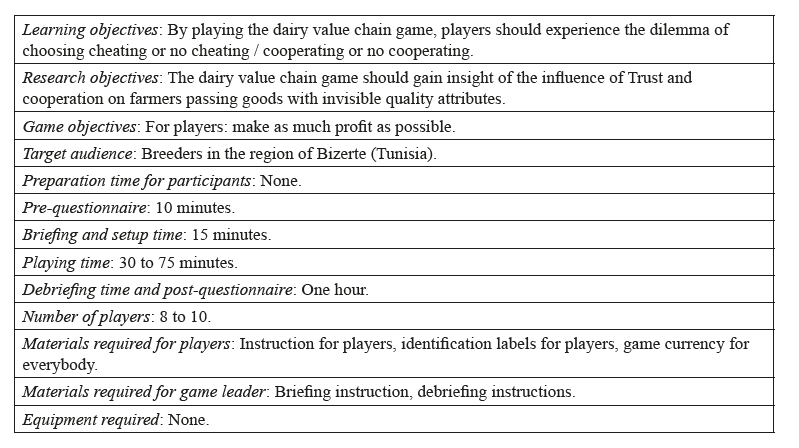
Abstract
The dairy value chain in Tunisia has been facing recurrent problems mostly related to coordination, contracting, pricing and quality imperfections. The policy focus on technology generation and dissemination, without considering the underlying problems related to market imperfections and institutional and socio-economic processes, has contributed to low technology adoption and limited development in the dairy value chain. This paper uses a gaming simulation approach to allow breeders to experiment and consider strategies of cooperation which lead to increased returns and improved quality of milk. The game allows understanding the role of trust and cooperation in improving the performance of the dairy value chain. The experiment was done in two regions and in four sessions each. Results show that benefits to breeders are derived from the price of milk which is determined by the number of cooperation in the repeated games strategies. The resulting Nash equilibrium is one where farmers cooperate without cheating. This solution avoids farmers the risk of rejection of milk and results in price increase as a result of the collective cooperative action.
DOI: 10.30682/nm1904c
Meriem Msaddak*, Jamel Ben-Nasr*, Lokman Zaibet*
* National Agronomic Institute of Tunisia, Tunis, Tunisia, Research unit in natural resource economics and agricolture (ERNA), Tunisia.
Corresponding author: msaddakmeriem@hotmail.fr
Cite this Item: Msaddak M., Ben-Nasr J., Zaibet L., Resolving recurrent imperfections in the dairy production using gaming simulation, New Medit, 18 (4): pp. 35-50, http://dx.doi.10.30682/nm1904c
1. Introduction
Imperfections in the dairy value chain in Tunisia include pricing mechanism, quality measurement and related information asymmetries, and overall market failure as a result of deficiency in coordination and organization. The lack of organization, coupled with the large number of stakeholders (small breeders, milk collection centers, large private producers, service providers, intermediaries, etc…), has led to malfunctioning of the value chain. The coordination problem is strongly linked to the absence of organization among the different agents in the value chain (Msaddak et al., 2017). The narrow policy focus on biophysical technology generation and dissemination, without considering the underlying problems related to institutional and socio-economic processes contributes also to low technology adoption and limits broader development in the dairy value chain.
Tunisia has employed several strategies aiming the development of the dairy sector. These strategies enabled Tunisia to achieve self-sufficiency in milk in 1999. However, in the successive strategies recurring problems (and related actions) remain unresolved. If inappropriate policies are implemented, it can influence the performance of the value chain (Sanz et al., 2015). Among these problems the organization of market participants and the development of a pricing system according to the quality and type of the product remain difficult to achieve. Contracting between the different actors (production and sale of milk and other animal products) stands as a major constraint in the dairy value chain management (Zaibet et al., 2005). In their analysis of the tomato value chain, Benmehaia et al. (2018) found that public policy have a role in the performances levels of the used vertical coordination mechanism by providing more incentive instruments. The lack of contracting and integration (“horizontal” and “vertical”) explains the failure to account properly for how value-chain analysis are mediated by factors relating to social relations, in addition to local history and environment (Jarosz, 2008). The informal system remains a true system of economic and social organization insofar as it manages to ensure joint coordination beyond the one-off market, by resorting to reciprocal agreements based on trust and oral contractual relations (Djermoun et al., 2014).
The most important socio-economic variables that affect the organization, coordination and overall performance of the dairy sector are trust and cooperation (Fink et al., 2010). According to Ramirez (2013), participation in producers’ associations has a significant impact on agriculture technology adoption and therefore plays an important role in knowledge transfer. Pali et al. (2013) examined the influence of networking on knowledge transfer and technology adoption, suggesting that producers’ knowledge level depends on the degree of networking in the community and is critical to promote adoption programs.
According to Krishnan and Winter (2013) supply chain management rests on the economics of contracts and game theory; imperfections in the economic conditions would be better dealt with by building contracts that optimally resolve the incentive distortions. The case in Tunisia is a situation where the contract system in the dairy value chain has been very slow. Cooperation through cooperatives and other farmers’ associations are instead sought to organize farmers to build market power, bargaining and to face other imperfections. This paper uses a gaming simulation approach to allow breeders to experiment cooperative solutions. Farmers would choose between “opportunistic” strategies and strategies of cooperation which lead to improved quality and price of milk and therefore increased returns to all participants. The experiment was done in two regions and in five sessions each. We designed this game based on the specificity of the research area. The paper is organized as follows: after this introduction (Section 1), we provide a short description of the dairy sector in Tunisia, followed by literature review (Section 2), methodology (Section 3). Results and discussion are presented in Section 4 and Section 5, followed by the main conclusions (Section 6).
2. The Dairy value chain in Tunisia and gaming simulation
The livestock sector has an important role in the country’s economy and in food security for strategic products such as milk and meat. It is also important because livestock is held by small farms and as such it plays a major role in income and poverty reduction in rural areas. On the economic side, the dairy sector contributes 11% of the total value of agricultural production, 24% of animal production and 7% of the value of the agri-food industry (GIVLait, 2014).
Most of the farms are small and practice extensive livestock farming. As a result, the growth of milk production has not followed that of processing capacity in the industry, which is the main reason for its disconnection from the local production sphere. The perishability of milk is a major difficulty, as it requires strict hygienic conditions for its preservation and transport in order to avoid bacterial contamination prejudicial to the health of consumers.
The dairy industry faces various constraints which hinder its development. These constraints are summarized as follows:
- Climatic Conditions
Tunisia is characterized by a great variability and climatic seasonality (temperature and rainfall). These extreme weather conditions are sources of risk to agriculture and livestock production. Indeed, periods of drought and flood often lead to loss of production and disruption of livestock activity due to lack of fodder and increased price of feed. Climate change will increase pressure on pastoralists and farmers in general.
- Production
The sector is characterized by land fragmentation and dispersal of livestock; the majority of farmers has small farm size. Farmers also have limited financial resources, which do not allow improving their technical level and developing their business. Another feature is the lack of professional organization of the small farmers. Breeders participation to cooperatives such as the Mutual Agricultural Services (SMSA) and Agricultural Development Associations (GDA) is still low (8%). The decline of natural pastures and the insufficient development of fodder crops have led to a shortage of fodder and increased use of concentrate feeds, made from imported raw materials which prices are constantly rising, therefore reducing the profitability of farms. The livestock production is also characterized by seasonality of milk production. All actors in the value chain are affected by the shortage of milk during the periods of low lactation, and by the losses during high lactation periods. The problem of poor quality is also recognized by all actors in the chain and explained by the negative impact of feed costs and feed rations.
2.1. Game theory and gaming simulations: a review of literature
Economics has been regarded as a non-experimental science. In just a few decades, the landscape of economic research has radically changed. In recent years there has been growing interest by economists to measure actors’ behavior, using experimental games. The use of experiments to study human behavior has a long history (Cardenas, 2016). Experimental economics involves experimenting with individual and/or collective actions and analyzing the results statistically (Petit, 2013). It is a science in development, rewarded in 2002 by two winners of the “Nobel Prize” economics, Vernon Smith and Daniel Kahneman, for the application of the experimental methods to economic science thus far used in psychology.
In addition to game theory, economic theory has other main branches like decision theory, general equilibrium theory, the theory of mechanism design… All are closely linked to gaming simulation, which is defined as «a methodology for relating the micro-level (agent-level) behavior to the macro-level (system-level) behavior» (Meijer, 2009). In short, game theory can include game theoretic models of agents’ behavior and interactions, and considers rules, roles, goals and constraints (Duke and Geurts, 2004). The game combines a repeatable experience with the ability to observe actors, transactions and the performance of a value chain. Repeatable experience allows comparing networks composed of different people having the same rules, roles, objectives and constraints. In real situations, farmers and processors are investing in specific relationships to ensure their supply and disposal of their products, especially when players in the value chain do not offer neither price guarantees, nor the agreed quantity and the quality of the products. Such specific relationships give rise to reputation which is acquired through behavior over time with frequent transactions (Williamson, 1993; Dasgupta, 2000). In the gaming literature we find many examples. In the experiment of Sterman (1989), subjects manage a gaming simulation of industrial production and distribution system called “beer distribution game” to minimize total costs. Barreteau et al. (2007) study simulation and gaming in Natural Resource Management Issues. Balzer and Brendel (2001) compare discrete social simulation with other methodologies used in the study of social phenomena.
The relationship between game theory and gaming simulations goes in both directions. Game theory provides an extremely useful background for the structuring, the building and analysis of games. Yet at the same time gaming provides important evidence for the construction of new solution concepts for games and for the isolation of sociological, psychological and other variables which are not taken into account in game theory such as trust between actors in the value chain. Cooperation in repeated games is primarily motivated by long-term payoff maximization and that even though some subjects may have other goals (Dreber et al., 2014). Empirically, cooperation rates are systematically associated with Prisoner game theory’ payoff structures (Glöckner and Hilbig, 2012). Kreps et al. (1981) show using the finite repetition of the prisoners’ dilemma that incomplete information about one or both player’s opinions, motivation or behavior can explain the observed cooperation. (Guyer and Perkel, 1972) studied the n-period game.
Game theory has been widely used in resource management and cooperation. Skardi et al. (2013) provide a wide overview of applications of game theory in conflict resolution. Jolly and Wakeland (2008) used a game theoretic framework to examine the interactions between individuals in an organization with different preferences, regarding knowledge sharing. Schreider et al. (2009) describes the application of game-theoretic approach with specific emphasis on developing optimal strategies of phosphorus applications for soil fertilization. Yaron and Ratner (1990) present an analysis of the economic potential of regional cooperation in water resources using cooperative game theory algorithms and shadow cost pricing. Most of the literature on game theory studied the n-period game and sub-games. However, the data generally indicate that cooperation rates drop shortly after the start of play, and after some delay where cooperation is not prevalent, the players move toward more cooperative choices (Rapoport, 1973). The importance of repetitions comes from the participants «equilibrium between short-term benefit and log-term benefit. When the game is conducted only once, each participant only concerns about one-time benefit. But if the game is repeated several times, people may be involved in the long term benefit at the expense of immediate benefit to choose a different equilibrium strategy (Brede, 2013).
This paper uses a gaming simulation approach to allow breeders to experiment cooperation, considering not only ‘opportunistic’ strategies but strategies of cooperation which lead to increased returns and improved quality of milk. Cooperation is primarily based on the ability of actors in the value chain to identify opportunities to interact with each other, assess issues, access social resources, and learn and share information (Rajalahti et al., 2008). The level of trust between partners determines cooperative behavior. In fact, the risks associated with cooperation, could be reduced when trust is high (Lui and Ngo, 2004).
3. Study area, experimental design, and data collection
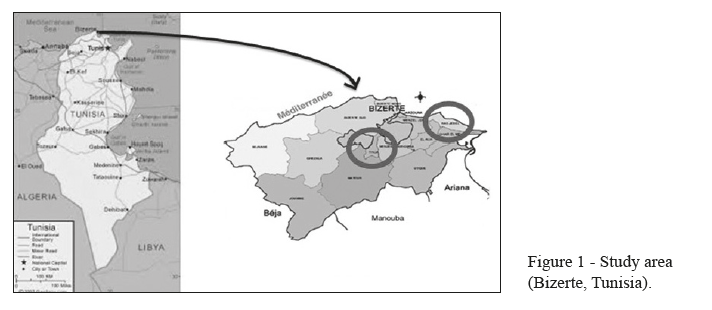
The experiment was done in two regions in the governorate of Bizerte in the north of Tunisia (Figure 1). The choice of the zone of study can be explained by the performance of the dairy value chain in this region which remains limited despite the abundance of natural resources and the large number of dairy breeders. Although the Bizerte region, which is part of the northern zone, Tunisia’s main agricultural region with 25% of the country’s land area, is the most fertile land and where rainfall is generally adequate with a tradition of foraging crops in Tunisia irrigated and natural watering, but we note that the average annual production is of the order of 2574 liters / animal / lactation against an average of 8000 liters in some European countries (case of France, Holland). A situation which reveals that the weakest link in the sector lies in its upstream part and that the profitability of the investment is often questioned.
The solution for some is to restock livestock (composed in 2017 of 52% pure breed and 33% cross breed & 15% local breed respectively with an average annual production per VL of 4163 & 1041 & 373 liters), improving production performance and developing new feeding techniques.
If we compare the organizations set up at the level of primary production, we can see that the performing countries in this area rely mainly on cooperative organizations and/or herders’ group, something that Bizerte lacks. In Tunisia, the large number of actors involved in the sale of milk produced on the farm (collection centers, large private or state producers, service cooperatives, collectors, etc.) has led to a malfunctioning of and jeopardized the quality of the milk. As this situation provoked the intervention of the State, which subordinated the milk collection premium to a set of specifications and subjected the collectors to a health certification, so as to guarantee the quality of the milk collected, the results remained below assigned objectives. Studies and politics suggest solving this problem.
Along the dairy value chain, we examine cooperation between farmers (the dilemma to cooperate or to sell their milk individually) and trust facing the dilemma (to cheat or not to cheat in the quality of milk). We study the decision making process to examine the behavior of the players and use the output of the game, a pre-questionnaire, and the debriefing of the game to understand the role of trust and cooperation in improving the performance of the dairy value chain. With the help of the game, participants can create a governance system that fits their needs. Usually, they start trading in individual transactions, and the game simulates a normal market. Once some farmers start cooperating horizontally this creates other market structures: for instance, by merging their firms producers can create a monopoly, which creates a hierarchy.
In this experiment, the player is able to make two decisions. The first is to choose to cooperate with which person and the second is to choose the quality of milk she decides to produce. . In the phase of negotiation, the players can talk to each other during one minute. After that, each one writhe his options in the card and give them separately to the animator. The players have to accept all the milk producers who want to join their cooperatives. The player who is producing less than 90% of high quality milk is considered to be cheating. The game is repeated 4 times (4 sessions) to study the change of the behavior of players following the previous session, which would show the importance of experience in the farmer’s decisions. Although the game is used to simulate a wide range of cooperatives, the most typically used consists of 10 farmers to play the game. All the players are small farmers with a herd of less than 10 dairy cows. If the game leader decides to enlarge the teams, the analysis of the game gets more complicated. One-man teams are equal to one-man cooperative, leaving out the difference between individual decision-making and team (cooperative) performance. Before starting the game, farmers answer a short questionnaire. We ask them questions about the relationship between players if they know each other and the level of trust following a 10 points Likert scale. There are also questions about the trust in cooperatives and in collection center, and whether or not they were involved in a cooperative.
Players in the game produce two different types of milk: high and low quality milk. We distribute 100 Tunisian dinars (TND)for each player. In this game, we are playing with fake money. Typically, we used cards where players write the percentage of high quality milk that they decided to produce and their preference to cooperate or not. If they choose to cooperate, they have to choose their partners in the cooperative. Each player pays the cost of milk produced. The cost of high quality is higher than normal quality. The price of the milk to sell is function of the number of players who want to join a cooperative. This choice can be explained by the formation of coalitions in cooperative games between the players to obtain the best possible result for each of its members. It is more of a competition between coalitions than between individual players. A concept used in cooperative games is the notion of characteristic function ν, which allows specifying a value for each coalition. For a finite set of n players called the grand coalition and denoted N, this function sends 2 N to R, and, for each coalition C (subset of N = {1, …, n}), ν (C) gives its maximum value.
In the end of the session, a bonus is given to the players or cooperatives that produced the best quality. The person or cooperative that has the best quality will have a bonus of 10 TND. We added this bonus to make use of the quality payment that is missing in the dairy value chain and can encourage farmers to produce good quality.
Then following the face that shows the dice and the percentage of high quality that produced the farmer, we accept or reject the milk. The basic data of the game are shown in the guideline (Appendix A). For example, if the face of the dice shows six, the collection center will refuse the milk of players who produce a high quality less than 90% (Appendix A). The dice game presents the probability of acceptance or rejection of the milk by the collection center. We added the dice game option referring to the problem of the periodicity of the milk production.
We introduce the dice game because in Tunisia there is a periodicity of dairy production. In the period of high lactation, the collection center is strict about norms of milk quality and the parentage of rejection milk is higher than in the period of low lactation. The dice game shows the probability of acceptance or rejection of milk by the collection center. In the game, the milk producers are paid following the face that shows the dice and the percentage of high quality produced. The basic data of the game are shown in the guideline (Appendix A). For example, if the face of the dice shows six, the milk produced with high quality less than 90% will be rejected. (Appendix A).
The game is played in two regions in the north of Tunisia. The difference between the two regions is:
- Region1: The players didn’t kwon each other from the beginning (Reputation = 0).
- Region2: The players know each other from the beginning (Reputation > 0).
The game will be repeated in 4 sessions. After each session, the game leader evaluates trust in a discussion with the participants afterwards. This reveals the reasoning and process of thinking of characteristic participants during the game. The sessions are not linked and the game starts from the beginning each round. At the end of the game, each player count the money left. The winner is the player who made the best profit.
4. Conceptual Model
In the study, our game is a dynamic cooperative game with incomplete and imperfect information. The player has to choose between two couples of decisions (Figure 2):
- Cooperate (sell the milk with other players) or not cooperate (sell the milk individually), and
- Cheat (produce less than 90% of high quality milk) or not cheat (produce more than 90% of high quality milk).
The repetition of a game with knowledge of intermediate results changes often fundamentally its unfolding. For example, it may be useful to occasionally take the risk of losing to test the reaction of others players and thus set up communication strategies by the actions played (in the absence of other means of communication). It also happens that reputation phenomena are developing, phenomena that will influence the strategic choices of other players.
Perfect information refers to the actions in the game and the complete information refers to the structure and winnings of the game.
The information is incomplete because players do not know if their milk will be rejected or accepted by the introduction of a dice game which represents the probability of rejection or acceptance of milk (incertitude).
The information is imperfect because players do not know the quality of milk produced by the other players.
4.1. Strategies
In our study, we used the game simulation data to estimate the utilities of players following Schreider et al. (2009):
The strategy set Si, i = 1, 2, … , n, available to each player is given by
![]()
where αi = the percentage of high quality produced by the farmer and ti= is the number of persons who choose to cooperate.
We allow αi to vary continuously within the interval A = [A1, A2] , i.e., irrespective of the player, there is a minimum quality A1 and a maximum quality A2.
We suppose the total quantity of milk produced is 100 liters each session. Similarly, the number of farmers in cooperatives, ti takes values in an interval T = [t1, t2] where t1 is the minimum time and t2 the maximum time of application.
For each strategy (αi, ti) ∈ Si and given the price of milk P(ti), the utilities are defined as follows:
- If acceptance:
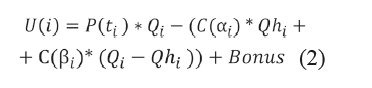
- If rejection:
![]()
where
Qi = total quantity of milk produced by the player i,
Qhi = quantity of high-quality milk produced by the player I
P(ti) =Price of milk, a function of the number of players in cooperatives
C = Cost of milk in cooperatives which is function of the quality of milk
βI = the percentage of low quality produced by the farmer
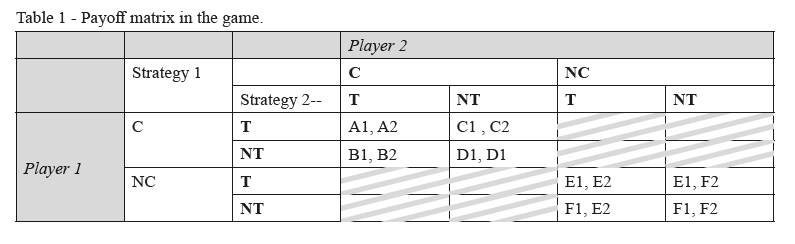
Table 1 shows the different gains of the players choosing the following strategies (shown also in Figure 1). In Table 1 the different letters are defined as follows:
- A1 (or 2) is the gain of the player 1 (or 2) choosing to cooperate and to cheat (C-T).
- B1 (or 2) is the gain of the player 1 (or 2) choosing to cooperate and not to cheat (C-NT) when player 2 (or 1) cooperates and cheats.
- C1 (2) is the gain of the player 1 (or 2) choosing to cooperate and cheat (C-T) when player 2 (or 1) cooperates and doesn’t cheat.
- D1 is the gain of player 1 and 2 when they choose to cooperate and didn’t cheat.
- E1 (or 2) is the gain of player 1 (or 2) when he doesn’t cooperate and cheats (NC-T).
- F1 (or 2) is the gain of player 1 (or 2) when he doesn’t cooperate and doesn’t cheat (NC-NT).
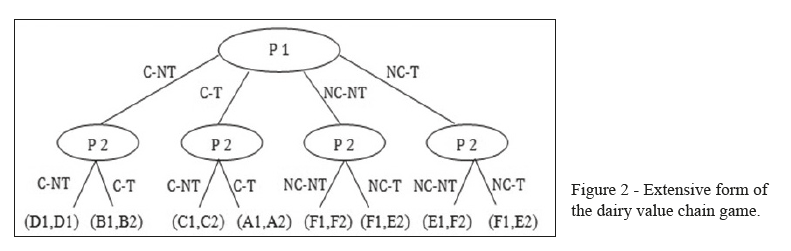
This game study trust between farmers in two levels:
- To trust in the quality of milk and do not cheat.
- To trust other players and cooperate with them.
5. Results of the game simulation
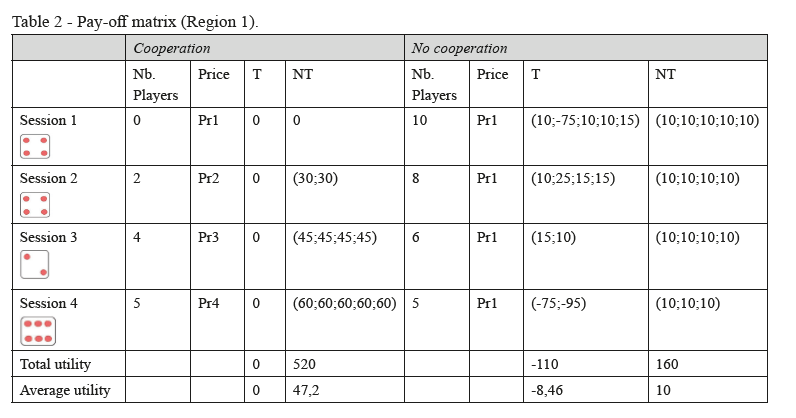
In the pre-questionnaire, we used a 10 points Likert scale to find out the trust of players in the different stakeholders in the dairy value chain. The results show that the levels of trust in participants (4.06), cooperative (2.77), collectors (3.56) and collection center (4.25) are under the average. However, we note that the most inferior level of trust is given to cooperative with an average of 2.7 which shows that breeders don’t trust cooperative. Results show also that breeders trust collection centers more than collectors. Based on the payoff matrix in Table 1, we regrouped the players per strategies and averaged the utility for each strategy. Results of the game in Region 1 and 2 are displayed in Table 2 and 3. To find out the best strategy, we calculate the average of player’s utilities of each strategy. The price (Pr1, …, Pr4) is function of the number of players in cooperative. (Appendix A) The highest utility (Average = 122.9 DT) is found for players who followed the strategies [Cooperate, Not cheat] during all four sessions. The number of players who cooperated increases from 0 in session 1 to 5 players in session 4. The total utility increases with the number of players in cooperative. Also, in the cooperation strategy no one of the players has chosen to cheat in the quality.
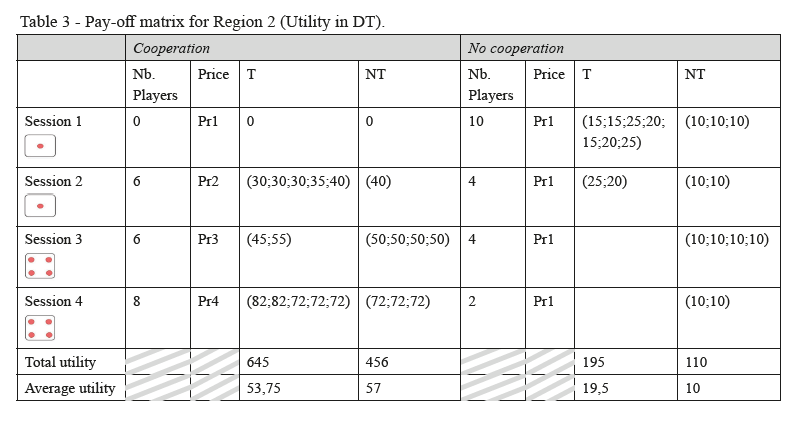
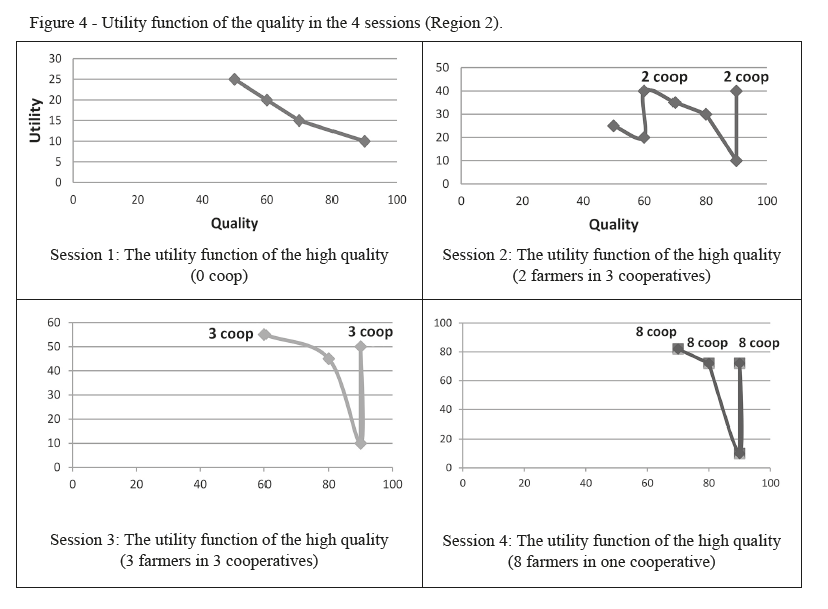
In Region 2 where players know each other, the results in Table 3 show that the strategy that is most efficient is the strategy [cooperate , not cheat]; it provides players a better utility (Average utility = 445 DT). The number of players who cooperate in this region is higher than that the Region 1 since players are neighbors and are used to deal with each others.
In the second session, the milk producers who cooperate (2 players) and produce high qualities (100%) have better utilities (30) than the producers who didn’t cooperate and produce less quality. In addition, one player of the cooperative cheated in the quality of milk in the first session then changed his behavior in the second session and produced a high quality of milk In the first region, the number of players who didn’t cheat is higher than the other region. In the region 1, the players didn’t want to take risk and they played individually.
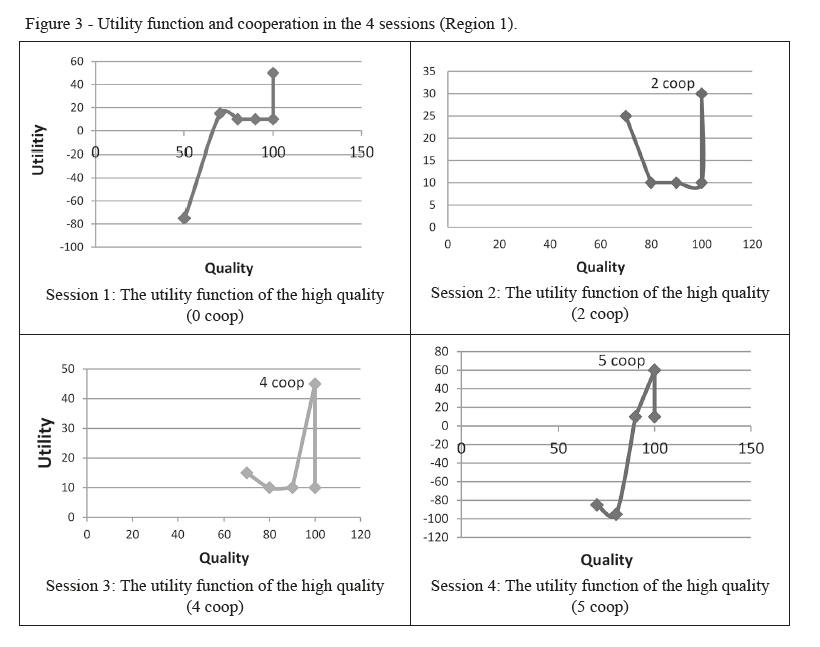
In sessions where players didn’t cooperate and cheat in the quality, their milk was rejected by the collection center and their utilities were negative (Total utility = -1250 DT) In the four sessions, the high quality of milk increases with the number of players in cooperative (Figure 3). This is show that cooperation reduces cheating and improves honesty and trust between farmers. In the first session, all breeders behave opportunistic (Number of cooperation = 0) which affect the quality for 50% of players. Besides, for the others players the utility decrease despite of high quality because of the high cost of high quality milk. In the second session players form 3 cooperatives, each one is composed of 2 players. In this session, all milk producers who cooperate increase their quality of milk. In the third session, the number of players who cooperate increases to 3 players in two cooperatives. In the third session we have a cooperative of 4 players and in the last session a cooperative with five players with the best qualities and utilities. In this game, the repetition had a positive effect on trust and cooperation since the cooperative overweighs all the sessions in the game.
6. Discussion
Based on the pre-questionnaire, the failure of cooperative system in the 1960’s in Tunisia could explain the low level of trust attributed to the cooperatives. In fact, at the beginning of 1967, collectivism was in full swing, but the cooperatives had not produced the desired results for two essential reasons: In the first place, small farmers were against divesting their property for the benefit of a cooperative where their status changed from owner to worker. This led to malpractices where some were enriched while those who had worked hard for the development of their land were overnight divested. This system had not affected the big farmers who had not been affected before. Second, during that period a bad economic situation coupled with a drought also affected the whole country. The indebtedness of these cooperatives was increasing. The situation was deteriorating day after day. Such a failure has had a negative impact on breeders who are now against cooperatives and cooperation (Boulet, 1971).
During the game, players didn’t know the decision of each other and all information is hidden in an envelope. The players didn’t know if the milk will be accepted or rejected by the collection center since it’s linked to a random process like the dice game. It’s a game with imperfect and incomplete information. The game is repeated in 4 sessions. Results show that cooperation between breeders increase during the four sessions. These conditions are conform to finite repeated game. This dilemma results in a Nash equilibrium at the end of the game where no player has interest to deviate.
In both regions, Cooperation and avoid cheating (C-NT) represents the dominant strategy for the players. Hence, there is no unilateral profitable deviation from any of the players.
In every stage of the game, cooperation and avoid cheating (C-NT) represents the dominant strategy for the players. there is no unilateral profitable deviation from any of the players. For repeated games with a fixed and known number of time periods, if the stage game has a unique Nash equilibrium, then the repeated game has a unique subgame perfect Nash equilibrium strategy profile of playing the stage game equilibrium in each round.
Therefore, the combined strategy (C-NT, C-NT) is a social optimum which is the profile that maximizes the sum of the players’ profits.
For example, in a society composed of two prisoners, the social optimal is cooperation, which is not a Nash equilibrium. Then, we consider the Generalised Nash Equilibrium, also called Coupled Constraints Equilibrium can be engineered that corresponds to social optimum. Here, players are given weights that may reflect how the regulator appraises each player’s output from a social point view (Contreras et al., 2015). As a conclusion, we consider the strategy (C-NT, C-NT) a Nash Equilibrium.
Therefore, the combined strategy (C-NT, C-NT) is a Nash equilibrium. This could be reasonable if there is a long interrelationship that leads players to form opinions about how others play. It could also be reasonable if there is a social convention or a consensus or an agreement adhered to by the other players. In other words, no player has the interest of unilaterally deviating if he correctly guesses the strategies of the other players. If a player looks at a strategy profile as a social convention, no player would want to deviate when he or she thinks the other players are following the convention.
To analyze the effect of both couple of strategies (cooperation (C), No cooperation (NC)) and (cheat (T), No cheat (NT)), we use the average gains realized by each breeder to determine the Nash equilibrium. So, we can recap the games in Table 4 for Region 1 and Table 5 for Region 2.
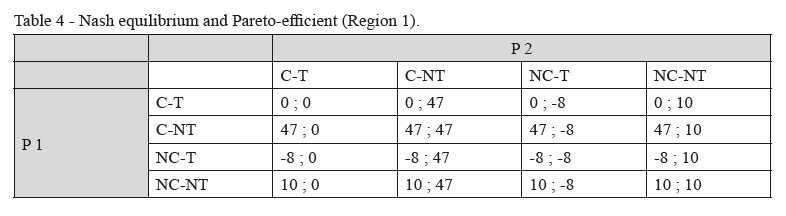
At the end of the game, the combination strategy (C-NT, C-NT) correspond to the payoffs (47;47) which is Pareto-efficient. According to results in Table 4, the amount 47 DT is the highest average of utilities for all players. For region 2, the combination strategy (C-NT, C-NT) is Nash equilibrium and payoff (57;57) is Pareto-efficient (Table 5). In this region, the average of utilities is higher than region 1 because in region 2 the number of famers involved in cooperative is higher. Even if deviations from reality have been revealed, the farmers consider that this schematic representation of the reality proposed in the game allows them globally to evolve as in the real value chain. They find there a certain number of rules they share with each other. The rules, behaviors, interactions and processes represented are not exhaustive.
These results are similar to the paper of Schreider (2009) who used a game in which he considers competitive strategies and strategies which imply cooperation between farmers and the economic advantages of phosphorus applications and the environmental losses associated with these applications expressed as dollar values. The results show that the cooperative solutions lead to much lesser environmental impacts and a better economic advantages than that in the case of non-cooperative strategies. The results of the game show the increasing of utility when switching from competitive to cooperative strategy just like in our game which demonstrates the benefits of cooperation.
7. Conclusions
Game theory is a rapidly advancing approach for analyzing conflicts. Game theory applications in resolving imperfections in the dairy value chain cover a range of problems in diverse categories and types and allow simulation of the self-centered attitude of the involved players with a fairly realistic manner. In the context of the dairy sector, game theory methods compared to other conventional methods of strategic analysis, such as linear programming, provide better understanding of issues describing the competition and cooperation between players and make better estimations of the conflict outcomes. The application of gaming simulation as a research method can be of value for gathering data about the real behavior of real participants in a simplified environment. In this paper, we demonstrate that a cooperative as an institutional arrangement can improve the quality of milk and increase the breeder’s income.
The dairy value chain in Tunisia has been facing recurrent problems mostly related to coordination, contracting, pricing and quality imperfections. The failure of cooperatives in the past had a big impact on the behavior of farmers who have lost confidence in cooperatives despite the many benefits they offer. The policy focus on technology generation and dissemination, without considering the underlying problems related to market imperfections and institutional and socio-economic processes, has contributed to low technology adoption and limited development in the dairy value chain.
The approach used in the paper is a gaming simulation where breeders consider strategies of cooperation in repeated sessions. The experiment was done in two regions with different settings, in particular where farmers know each other or not. Despite their background farmers formed cooperatives changed their strategies during the game sessions. For the first session, all farmers have a timely opportunistic behavior, but during the game they gradually communicated and cooperated to earn more profit and win the game. In fact, the success of the cooperatives from one session to another encouraged other farmers to cooperate. This study is not only intended to study the impact of cooperation on milk quality and profit but it is a method of popularizing farmers to think in the future to cooperate in the aim of reducing costs and improving their income.
The repetition in the game simulates experience and reputation in the real world. In fact, the number of repetitions affects positively the level of cooperation and high quality milk. Hence, cooperation and collective action improve trust between breeders. Indeed, the combination of strategies (cooperated and not cheated; cooperated and not cheated) corresponds to a situation of Nash equilibrium and Pareto-efficient. As a participatory approach, players were convinced in the debriefing that cooperation can improve their milk quality and profit. This cooperation can be facilitated, legitimated and institutionalized by a social contracts and consensus.
Our findings have significant policy implication which can improve the management of the dairy sector and value chain; farmers are now willing to improve the quality of milk according to the payment to quality scheme. During the debriefing, breeders reclaimed this option (which is the bonus attributed to the best quality in the game). Our study focused on cooperation and trust related to quality of milk, but cooperation can be affected by other social factors. This implies a need for further empirical research that includes other characteristics, norms and values explaining the choice to cooperate and the governance mechanisms in general.
References
- Balzer W., Brendel K.R., 2001. Bad arguments in the comparison of game theory and simulation in social studies. Journal of Artificial Societies and Social Simulation, 4(2): 1.
- Barreteau O., Le Page C., Perez P., 2007. Contribution of simulation and gaming to natural resource management issues: An Introduction. Simulation & Gaming, 38(2): 185-194, ISSN: 1046-8781, DOI: 10.1177/1046878107300660.
- Benmehaia A.M., Brabez F., 2018. Vertical relationships and food supply chain coordination: The case of processing tomato sector in Algeria. New Medit, 17(2): 3-14.
- Brede M., 2013. Short Versus Long Term Benefits and the Evolution of Cooperation in the Prisoner’s Dilemma Game. PLoS ONE, 8(2): e56016, DOI: 10.1371/journal.pone.0056016.
- Cárdenas J.C., 2016. Human behavior and the use of experiments to understand the agricultural, resource, and environmental challenges of the XXI century. Agricultural Economics, 47: 61-71, DOI: 10.1111/agec.12311.
- Contreras J., Krawczyk J.B., Zuccollo J., 2016. Economics of collective monitoring: a study of environmentally constrained electricity generators’, J. Comput Manag Sci, 13: 349, https://doi.org/10.1007/s10287-015-0247-9.
- Dasgupta P., 2000. Economic Progress and the Idea of Social Capital. In: Dasgupta P., Serageldin I. (eds.), Social Capital: A Multifacted Perspective, World Bank, Washington, DC.
- Djermoun A., Belhadia M., Chehat F., Bencharif A., 2014. Les formes de coordination entre les acteurs de la filière lait au niveau de la région de Chéliff. New Medit, 13(3): 39-49.
- Dreber A., Fudenberg D., Rand D., 2014. Who cooperates in repeated games: The role of altruism, inequity aversion, and demographics, Journal of Economic Behavior & Organization, 98: 41-55.
- Duke R.D., Geurts J.L.A., 2004. Policy games for strategic management. Amsterdam: Dutch University Press.
- Emami Skardi M.J., Afshar A., Sandoval Solis S., 2013. Simulation Optimization Model for Non-point Source Pollution Management in Watersheds: Application of Cooperative Game Theory, KSCE Journal of Civil Engineering, 17(6): 1232-1240, DOI: 10.1007/s12205-013-0077-7.
- Fink-Hafner D., Lajh D., Deželan T., 2010. The open method of coordination in the global context of policy cooperation. In: Fink-Hafner D. (ed.), The open method of coordination. Ljubliana: Faculty of Social Sciences, University of Ljubljana, 17-34.
- Glöckner A., Hilbig B.E., 2012. Risk is relative: Risk aversion yields cooperation rather than defection in cooperation-friendly environments. Psychonomic Bulletin & Review, 19(3): 546-553.
- Guyer M., Perkel B., 1972. Experimental Games: a Bibliography (1945-1971). University of Michigan Mental Health Research Institute Communication, 293.
- Kreps D.M., Milgrom P., Roberts J., Wilson R., 1981. Rational Cooperation in the Finitely Repeated Prisoners’ Dilemma. Journal of Economic Theory, 27: 245-252 (1982).
- Krishnan H., Winter R.A., 2012. The Economic Foundations of Supply Chain Contracting, Foundation and Trends R in Technology, Information and Operations Management, 5(3-4): 147-309, 2011[14].
- Jarosz L., 2008. The City in the Country: Growing Alternative Food Networks in Metropolitan Areas, Journal of Rural Studies, 24(3): 231-244.
- Jolly R., Wakeland W., 2008. Using Agent Based Simulation and Game Theory Analysis to Study Information Sharing in Organizations – The InfoScape, Proceedings of the 41st Hawaii International Conference on System Sciences.
- Lui S.S., Ngo H.-Y, 2004. The Role of Trust and Contractual Safeguards on Cooperation in Non-equity Alliances. Journal of Management, 30(4): 471-485.
- Meijer A., 2009. Understanding modern transparency. International Review of Administrative Sciences, 75(2): 255-269.
- Msaddak M., Ben-Nasr J., Zaibet L., Fridhi M., 2017. Social networks for the sustainability of the dairy sector: the role of cooperatives, Livestock Research for Rural Development, 29(2).
- Pali P.N., Zaibet L., Mburu S.K., Ndiwa N., Rware H.I., 2003. The potential influence of social networks on the adoption of breeding strategies. Livestock Research for Rural Development, 25(5), Article #89. Retrieved from: www.lrrd.org/lrrd25/5/pali25089.htm.
- Petit E., 2013. L’économie du care. Presses Universitaires de France, «Care studies», 60 pages, ISBN: 9782130624646, DOI: 10.3917/puf.petit.2013.01, https://www.cairn.info/economie-du-care–9782130624646.htm.
- Rajalahti R., Janssen W., Pehu E., 2008. Agricultural innovation systems: from diagnostics toward operational practices. Agriculture & Rural Development Department, World Bank, Washington, DC.
- Ramirez A., 2013. The Influence of Social Networks on Agricultural Technology Adoption, Procedia – Social and Behavioral Sciences, 79: 101-116, ISSN: 1877-0428, https://doi.org/10.1016/j.sbspro.2013.05.059.
- Rapoport A., Kahan J.P., Stein W.E., 1973. Decisions of timing in conflict situations of incomplete information, Systems Research and Behavioral Science, 18(4): 272-287.
- Sanz-Cañada J., García-Brenes M.D., Barneo-Alcántara M., 2015. Value Chain and Typicity Analysis in Jaén Mountain Olive Oil, Spain. New Medit, 14(3): 50-60.
- Schreider S., Zeephongsekul P., Fernandes M., 2009. Modelling the Optimal Strategies of Fertiliser Application Using the Game-Theoretic Approach, Environ Model Assess (2010) 15: 223-238, DOI: 10.1007/s10666-009-9202-x.
- Sterman J.D., 1989. Modeling managerial behavior: Misperceptions of feedback in a dynamic decision making experiment. Management Science, 35(3): 321-339.
- Williamson Ó., 1993. Calculativeness, Trust, and Economic Organization. The Journal of Law and Economics, 36(1): 453-486.
- Yaron D., Ratner A., 1990. Regional cooperation in the use of irrigation water: efficiency and income distribution. Agricultural Economics, 4(1): 45-58.
- Zaibet L., Salem H.B., Bachta M.S., 2005. Analyse de la décision contractuelle des producteurs du lait en Tunisie. Tropicultura, 23(3): 154-161.
Annexes
Annex A – Dairy value chain game guideline

Annex B – Basic Data of the game