An optimal price for sustainable irrigated agriculture in central-eastern Tunisia

Abstract

Increasing pressures on water resources are causing many countries in Mediterranean to (re)consider various mechanisms to improve water use efficiency for agricultural like Tunisia country. The price mechanism remains the most appropriate instrument to allocate this water resource, but the search for the optimal price of water that reconciles different aspects economic and environmental is the most important issue to rise. In this paper, we will show that the search for a compromise between farm income and water consumption is possible through an optimal price applying both the entropy maximization approach and the multiobjective optimization. The results show that the use of Generalised Maximum Entropy (GME) approach is able to calibrate the model. Once the model is calibrated, a Multi-Objective Programming (MOP) was used to determine the optimal price using the compromise method. This optimal price determined has resulted to a slight economic decline in agricultural income against an immediate environmental gain of water saving. This compromise is a way to ensure the sustainability of irrigated agriculture and the preservation of water resources in Tunisia.

DOI: 10.30682/nm1902a

Houcine Jeder*, Emna Ben Hamza**, Hatem Belhouchette**

* Regional Center of Research in Horticulture and Organic Agriculture (CRRHAB), Sousse, Tunisia / Laboratory of economy and rural communities, Arid Regions Institute (IRA), Medenine, Tunisia.

** International Center for Advanced Mediterranean Agronomic Studies (CIHEAM), Montpellier, France.

Corresponding author: djederhoucine@yahoo.fr

Download PDF

Cite this Item: Jeder H., Ben Hamza E., and Belhouchette H., An optimal price for sustainable irrigated agriculture in central-eastern Tunisia,  New Medit, 18 (2): pp. 3-14, http://dx.doi.org/10.30682/nm1902a

1. Introduction

During the last 30 years, irrigated agriculture in Tunisia has increased from 250,000 ha in 1990 to 450,470 ha in 2010 (MARH, 2013). Although the irrigated areas represent only 8% of the total agricultural surface, irrigation contributes with 35% of total, agricultural production and 20% of agricultural exports. The growth of the agricultural production in the recent years is mainly due to the expansion of irrigated areas (Al Atiri, 2009). However, the increase of irrigated areas has clear consequences on the country’s water resources. In fact, the intensification and use of chemicals and pesticides to increase agricultural production has led over time to groundwater overexploitation and land degradation (Louhichi, 2001). Today, some problems, such as declining fertility, salinity and soil erosion, have become major constraints to the sustainability of agricultural activity, particularly irrigated agriculture in Tunisia. Considerable efforts have been devoted to introduce policies tools aiming to reach a sustainable irrigation water management (Jeder et al., 2014).

Therefore, the new strategy introduced in the nineties has turned to the management and regulation of demand, while continuing the effort of water mobilization (Bachta et al., 2004). The main objective for this strategy is to conserve water resources and encourage demand management in the irrigation sector. Indeed, water pricing is considered one of the most important economic tools in the water demand management strategy; it has remained for long time largely subsidized and not reflects the reality of the resource production costs (Chebil et al., 2010). The pricing policy remains the most appropriate instrument to allocate this water resource, but the search for an optimal water price that reconciles two conflicting objectives (economic and environmental) is the most pertinent question to be solved.

According to the economic theory, the farmers would respond to the rising of water prices by reducing their consumption, according the negative slope curve demand. However, in the case of irrigation water, this reaction is not always true. Several studies showed the elasticity of water demand one beyond a certain threshold will become responsive to increase water pricing (Varela-Ortega et al., 1998; Berbel and Gomez Limon, 2000; De Faiture and Perry, 2002). The same issue and recommendations have been raised in several research papers in irrigated agriculture in Tunisia (Sghaier, 1995; Thabet, 2003; Chebil et al., 2010; Jeder et al., 2014).

The most important issue in water pricing policy is the optimal price determination that presents a certain trade-off between the farmer’s income and the irrigation water saving in order to maintain the sustainability of the irrigated agriculture in Tunisia.

This paper is a contribution to the study of the impact of water pricing policy on water demand at the farm level. We determine the optimal price to maintain the sustainability of irrigated agriculture through a certain compromise between the income of the farmer and the saving of irrigation water. A Generalised Maximum Entropy (GME) approach was used to calibrate the model followed by a multi-objective model to determine the optimal price which corresponds to a compromise between the farmer’s income and the water saving of irrigation to assess impact of this price at the farm level.

The document is organized as follows: The next section is the methodology adopted for this work. It is based on Generalized Maximum Entropy (GME) approach and Multi-Objective Programming model (MOP) accompanied by a brief description of the case study. The section three presents and discusses the empirical results. Finally, the concluding comments are presented in section 4.

2. Research Methodology

In order to have a detailed quantitative analysis, the mathematical programming model has long been used as the appropriate methodological framework for any aspect of agricultural economics modeling; because their structure is well adapted to the problem of the optimal use of limited resources. Economic agents are perceived as optimizers, and the basic elements of neoclassical microeconomic theory can easily be considered, as well as those of other economic theories, such as the theory of duality (Buysse et al., 2007).

Recently, the development of the Positive Mathematical Programming (PMP) initially proposed by Howitt (1995) for calibrating models was behind this renewed interest in mathematical programming models. Despite, this interest acquired, certain limits of Positive Mathematical Programming (PMP) were raised in their applications. The (PMP) requires zero degrees of freedom in the calibration constraints, which is very demanding in data or puts restrictions on the flexibility of the model’s functional form. Another limitation is that different procedures for obtaining calibration parameters lead to significant differences in simulation behaviour (Heckelei and Wolff, 2003).

In order to overcome these limits of the Positive Mathematical Programming (PMP) and to obtain more realistic simulation behavior, Generalized Maximum Entropy (GME) approach is a valuable alternative to the (PMP) model. This approach has been widely used in many agricultural economics research project for calibration model (Fragoso and Marquis, 2015) and adapted to empirically estimate crop-specific production technologies in Chinese agriculture (Zhang and Fan, 2001).

Heckelei and Wolff suggest a general alternative to the PMP based not on calibration, but on estimation of a programming model by Generalised Maximum Entropy (GME). In order to avoid some methodological problems, it directly employs the optimality conditions of a desired programming model to estimate simultaneously dual values of resources and calibration parameters, and we start this approach of (GME) with the quadratic term of the cost function of the following form like equation (1):

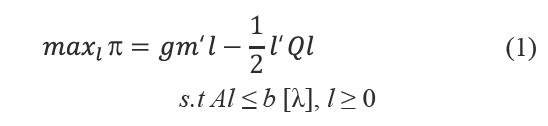Where π is the short-term profit function, which corresponds to the farm’s gross margin, gm and l are n×1 vectors of unitary gross margins per activity and non-negative variable of land allocation to crops, respectively; A is the m×1 vector of unitary resources requirements, b is the m×1 vector oh the availability of resources of resources, such as fixed resources (land) and variable resources (chemicals, labor and water), and λ is the m×1 vector of the corresponding shadow prices.

The basic principle of this approach can be illustrated writing the programming model in its lagrangian form (Equation 2):

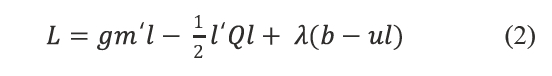
Where land is the only fixed resource, the matrix A = u , and u is n×1 summation vector ones. The first order optimality conditions are the zeros of the gradients of l and λ:

Thus, the unknown parameters λ and Q of these Kuhn Tucker conditions can be estimated using some econometric criteria. In this case, as the number of observations available was lower than the number of parameters to be estimated with this being hence an ill-posed problem, we applied the Generalised Maximum Entropy (GME) approach (Golan et al., 1996). Heckelei and Wolff incorporate some information about elasticities out the sample to have better estimates (2003).

The GME model applied to the optimality conditions of the programming model is given by following expressions:

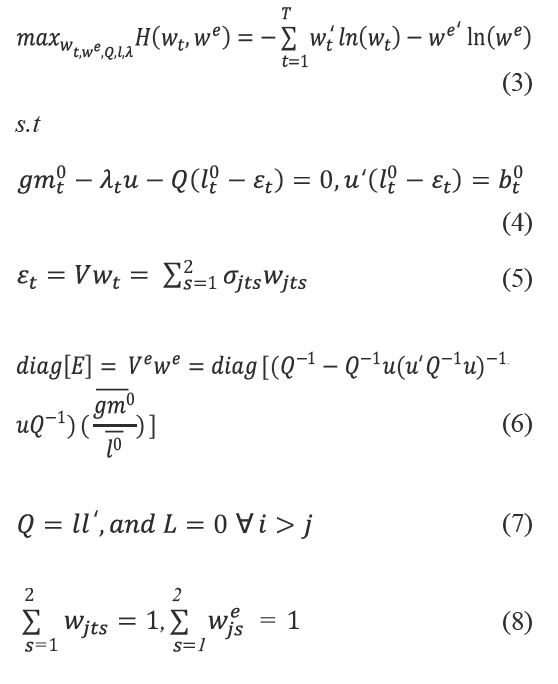
Where H is the Entropy variable; w_t and w^e are the probabilities with respect to estimates of the error (ε_t) and elasticity (E);  and  are known vectors of crops gross margin and crop level in each observation t, respectively; λ is the estimate of fixed resource (land) or shadow price; Q is the symmetric positive definite matrix of crop marginal cost coefficients; and V and V^e are the know matrix of error and elasticity support values, respectively.

Equation (3) represents the maximisation of joint entropy of the error and elasticity probability estimates. The first set of constraints (4) concerns the first order conditions of optimality. Equations (5) and (6) allow calculation of the valuation of error (ε_t) and elasticity (E). Variable cost function must be non-decreasing, and to meet the suitable curvature, the positive definiteness of Q is based on a Cholesky factorisation, which is present in equation (7). Finally, we have the set of equations (8), which assure that the sum of error and elasticity probabilities are equal to one.

The stochastic errors of each observation (ε_t) have zero mean and a standard deviation of σ_jts. To apply the GME approach, it was necessary to carry out re-parameterisation of the error term as expected values of a probability distribution (Vw_t). This is calculated based on know values of standard deviation, which are spread by tow support points (the n×m×2V matrix). Incorporation of out of sample information through the use of priors on elasticities allows us to obtain more accurate estimates for the Q matrix. As for the error estimates, the elasticities (E) also have to be re-parameterised as the expected values of a probability distribution (we). In this case, for the central value of prior elasticities two support points were also considered and the values of standard deviations are bounded in the (n×n×2V^e) matrix. After estimating the values of wt, we, ε t, Q and λ, the values of Q were incorporated into the programming model defined in (2), and which was used to assess the impact of optimal water pricing at the farm level.

Before assessment impact of water pricing in this paper, a Multi-Objective Programming model (MOP) is developed to determine the optimal price of water. The key of idea is to maximize profit and minimize water consumption, so as to preserve the water resources. The Non-Inferior Set Estimation (NISE) technique is used to generate the trade-off curves between these two objectives (Mimouni et al., 2000). These trade-off curves will help to determine a kind of water saving by reducing consumption. Finally, the compromise technique is used as a tool to determine the set of Pareto optimal solutions nearest to the ideal point which corresponds to the optimal price of irrigation water.

The multiobjective programming model applied is given by following expressions:

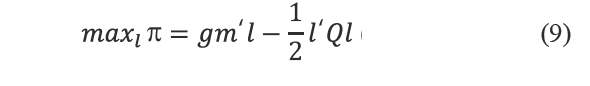
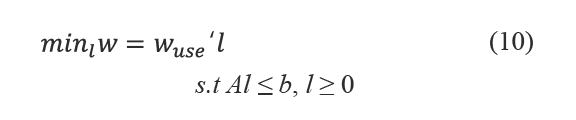
Where w is the total of water consumption by farm; gm, w_use and l are n×1 vectors of unitary gross margins, water use per activity and non-negative variable of land allocation to crops, respectively; A is the m×1 vector of unitary resources requirements, b is the m×1 vector oh the availability of resources of resources, such as fixed resources (land) and variable resources (chemicals and labor).

Among the different techniques to generate the efficient set, a variant of the weighting method has been chosen known as non-inferior set estimation (NISE) method, as the most suitable multiple objective programming technique for generating the efficient set (Cohan and Marks, 1975). To obtain compromise solution from the efficient sets, the degree of closeness, d_j between the j_th objective and its ideal value has been calculated and it was made unit free by taking relative deviation as under:

Where

d_j: degree of closeness between the j^th objective

z_j(x): the j^th objective function to be maximized or minimized

z_j^*: the ideal value of the j^th objective function

z_j⁺: the ideal value of the j^th objective function

The best compromise solution to the ideal point can be obtained by solving the following linear programming problems:

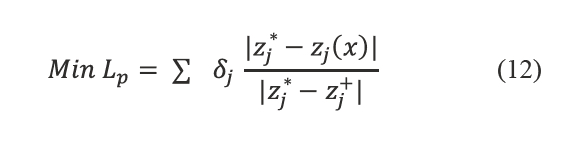
Subject to (X) ε F

Where (x) is a vector of the decision variables and

F: the set of all feasible farm plans

L_p: the distance function between each solution and its ideal point

δ_j: weights the importance of the deviations of j^th objective from its ideal value

P: weights of the deviations according to their magnitudes

L _(p=1) and L _(p=α) metric define a subset of the compromise sets.

The compromise programming approach find the optimum point for all the objectives and the compromise solutions for L1 and Lα formulate the bounds of the compromise set. Different set of the solution can be obtained by varying the weights given to the different objectives. Farmers/policymakers can choose any one solution for given preference of the different objectives out of the various compromise solutions (Singh and Jakhar, 2018).

Case study and data

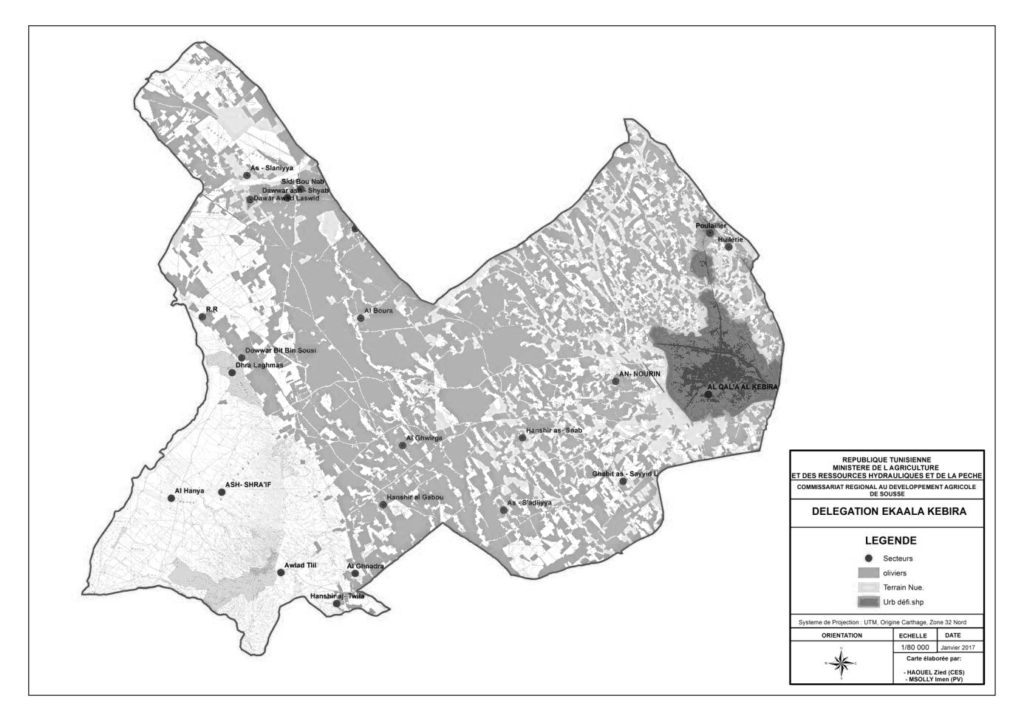
The data used in this study were collected from 65 farmers in the region of Kalâa Kebira located in the governorate of Sousse in Center-East of Tunisia (Figure 1). The main water source of this irrigated area is transferred from Nebhana dam, but the water scarcity is an important problem especially in recent years with the context of climate change. Irrigation water prices are almost the highest in the governorate. The price is approximately 0.16TD/ m³, whilst supplies in some other regions of Tunisia are priced at a minimum rate of 0.04 TD/ m³.Volumetric water pricing is applied in the irrigated perimeter of Kalâa Kebira. The scarcity of water resources is a limiting factor for irrigated agriculture in this region. The farmers are obliged to look for other alternative sources of water in adverse weather conditions to irrigate their crops so that their economic losses are not very high after a large investment made at the beginning of the season.

The Kalâa Kebira perimeter was created in 2003; it is mainly occupied by the potato on large surfaces in rotation with other vegetable crops such as pepper and tomato. These crops are intercropped with the olive feet. This perimeter occupies an area of 540 ha and is managed by the Agricultural Development Group (GDA).

Survey data used

The survey was carried out in 2017 on a sample of 65 randomly selected farms. The questionnaire is composed of two main parts: (i) a farmer’s identification about socio-economic and demographic characteristic and (ii) a farm’ identification about a management practice crops, amounts and costs of inputs; quantities and value of outputs, etc (Ben Hamza, 2017).

The main crops are vegetables and arboriculture. 43% of the average total area is occupied by potato crops with an area of 3.83 ha. This crop is grown in rotation with tomato crops which has 26% with an average area of about 2.26 ha, or with pepper crops which has 17% with an average area of about 1.5 ha. These crops are found in intercropping with arboriculture, particularly the olive tree. The area of the latter is of the order of 1.24 ha representing 14% of the average total area of the sample (Table 1).

3. Findings and discussion

GME model calibration

Before doing to used Multi-objective Programming Model and water policy simulations, model calibration tested by comparing the results of the crops allocation simulated by the Generalized Maximum Entropy (GME) model (simulated values) and the crops observed in the base year situation in 2017 (observed value).

Generalized Maximum Entropy (GME) model is applied to a representative average farm of 65 farms surveyed in the Kalâa Kebira region. The average size on the farm for the sample was 8.83 ha. This “average farm” is only a representative farm type of the studied perimeter of Kalâa Kebira.

All the data used in the model are related to input prices and outputs of production activities and the constraints of the resources used. These data are obtained from survey data (total land, irrigable land, labor, water, agricultural inputs).

The difference between land use values by crops for the current situation and after calibration with GME is measured statistically by percentage absolute deviation (DAP). The GME model does not exactly reproduce the observed situation; it is not like the case of the PMP method which reproduces exactly the observed situation (Louhichi et al., 2014). Small differences have been raised in GME model calibration through the calculation of Absolute Deviation Percentage (DAP) in Table 2. The land allocation to olives trees (0%) and other irrigated crops, such as potato crops where the PAD is important (5.14%) while it is lower for the tomato crop (14.21) and minimal for the pepper (0.55%). The totals of land and water used (0%) indicating that all constraints of resource availability are saturated with an entropy value is 2.01 and high shadow price land of 5579.60 DT (Table 2). Although the results for the PAD values show some differences, but they are small and do not exceed 15%, with a constraint of the land used is saturated (PAD of total land used = 0), so the calibration of the GME model is considered acceptable with these conditions.

Results of the Multi-Objective Programming model (MOP)

After the GME Model has been calibrated and validated, the multiobjective programming model was applied. First, each of two objectives was been optimized separately subject to the same constraints sets. The obtained values of each objective in the extreme optimal solutions are shown in Table 3.

The pay-off matrix obtained in the Table 3 indicates that the gross margin can vary between 55093.96 (DT) and 64558.22 (DT). Water consumption decreases from 38.40 (1000 m³) m³ to 34.85 (1000 m³), the highest value corresponding to the maximization of the gross margin. When the objective function is the minimization of the consumption of water, we notice that the possibility of saving water is possible with an economic loss of gross margin. This economic loss may be important, it is around 14.66% against the economy of water is 9.24% (Table 3).

This difference can be explained (i) by the use of the GME approach and the nonlinear cost constraints that make the model rigid and the constraint of land availability is always respected and (ii) the competitiveness of the use water between crops becomes important when the objective is minimization of water consumption. So the model will keep the crops the most competitive and profitable. For this, the minimum consumption was not zero because of the presence of calibration parameters and also the constraint of irrigable land which made the model a little robust to variations of variables.

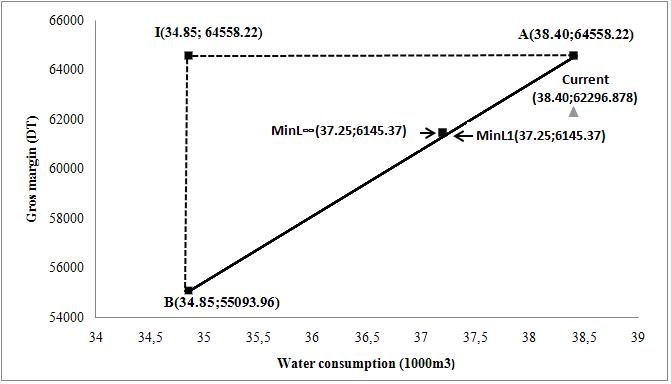
Figure 2 shows the trade-off curve between gross margin and consumption water. Using the NISE method, a set of optimal solutions has been identified between the extreme points (A and B) (Romero and Rehman, 1989). To reduce the set solutions, the compromise technique was applied with the weight for the gross margin maximization objective function is equal to the unit (w₁ = 1) and the weight of the objective function of minimizing water consumption is equal to the inverse of the slope coefficient of the trade-off curve

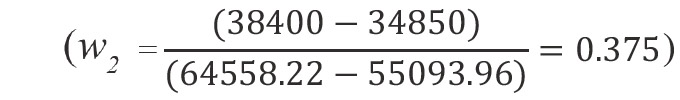
The L1 and L∞ solutions constitute the boundaries of the compromise set. This compromise solution C is nearest solution to ideal solution (Figure 2).

Water consumption is decreased from 38.40 (1000 m³) to 37.25 (1000 m³). This implies a saving of water of about 3.12% compared to the current situation. The reduction of water consumption implies economic losses about 1.35% compared to gross margin of the current situation (Table 4).

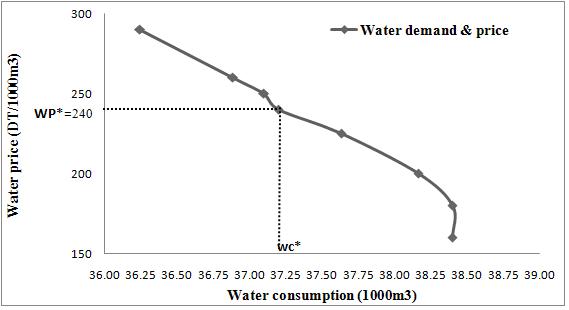
To determine the optimal price corresponding to the solution found by the compromise model, the passage through the water demand function was necessary. Figure 3 presents the derived water demand curve estimated with the GME model. This water demand curve is a little smooth showing several points of deviation with a weak slope. This can be explained by the strong constraint of land that was imposed by the calibration model and the high competition around the use of water by different irrigated crops. This demand curve better expresses farmers’ behavior to changes in the pricing policy. Indeed, when the consumption is 37.25 (1000 m³) case of compromise model results (C = WC*), the corresponding optimal price (WP*) is about 240 DT.

This optimal price leads to a slight economic decline in agricultural income of 95.52 DT/ha against an environmental gain in water saving of 0.136 (1000 m³). At the public perimeter having an agricultural area of 580 ha, this compromise provides for the future generation 78.88 (1000 m³) against a loss of agricultural income of 1.35%. A monetary gain for the Agricultural Development Group (GDA) equals 12620.8 DT which can be allocated for the maintenance and repair of hydraulic networks in case of failure. This compromise may be acceptable to maintain the sustainability of irrigated agriculture in the Kalâa Kebira region. The application of this optimal price generates an opportunity cost in terms of saving water by favoring the most profitable crops and the least water consuming.

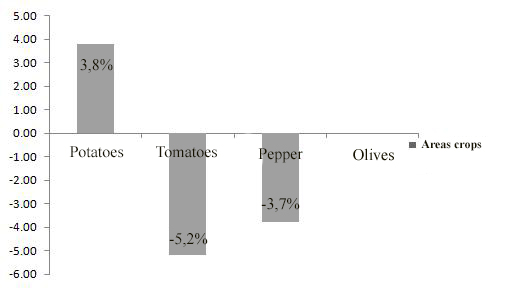
The Figure 4 shows that the optimal price application resulted in an increase 3.8% in area of ​​potato crops against a decrease of 3.7% and 5.2% respectively for pepper and tomato crops.

The area of arboriculture (olive tree) is constant, it is a restriction introduced into the constraint of the model. Arboriculture is a perennial crop and represents a major component of intercrop production system characterizing the study area that associates vegetable and arboricultural crops. Arboriculture contributes significantly to the income of farmers knowing that it indirectly benefits from the amount of water allocated to vegetable crops.

On the other hand, this type of associated production systems between arboricultural and vegetable crops can lead to long-term environmental and phytosanitary disadvantages, with the intensive use of chemical inputs and pesticides.

The choice of potato crop by the economic model is also justified by the answers of the farmers questioned saying that this crop is the most adaptable to the conditions of the availability of water at the public perimeter despite the high cost of seed in recent years.

The pricing policy is an effective economic instrument for reducing water consumption and applying an optimal price of water can lead to a compromise between the economic and environmental objective ensuring the sustainability of irrigated agriculture. The economic instrument of water pricing is necessary but it is insufficient. In certain cases, it may lead to some sort of specification of agricultural production for certain profitable crops, particularly at the regional level, where farmers are mainly subject to the same water constraint. This specialization will create an imbalance in the local market between supply and demand for other agricultural products not practiced by farmers. Thus an asymmetric transmission of prices between the regional markets will characterize the marketing circuit of these products with very high prices as the case of pepper this year.

Another point that must be made, the context of climate change which is characterized by the scarcity of rainfall and the decrease in recharge of groundwater aquifers, the price of water becomes a limiting factor of the second rank. The primary limiting factor is the availability of water (number of water towers) at the farm level, which forces farmers to see other alternative sources of irrigation water.

These results are in accordance with the results of other authors (Arabiyat et al., 2011). El Chami et al. (2011) show that volumetric tariff could be an effective tool to control water demand depending on yearly water availability; it could be very profitable to the irrigated perimeters to increase their financial returns. The most important other than the application of volumetric tariff is to find an optimal price that allows maintaining a compromise between farm incomes and water saving remains the most appropriate instrument to ensure the sustainability of resources in water and irrigated agriculture in this region.

4. Conclusion

This paper is a contribution to seek an optimal pricing of irrigation water in the public perimeter of Kalâa Kebira in central-eastern Tunisia. The aim of the research is to find an optimal price that corresponds to the trade-off between the economic objective of maximizing gross margin and the environmental objective of reducing water consumption through multi-objective modeling.

Before applying multi-objective modeling, the calibration of the model to reproduce the current situation of area allocation by crops was necessary and the use of entropy maximization model was mobilized for this purpose. The entropy maximization model has succeeded in reproducing the current situation and the calibration is considered acceptable.

The application of the multi-objective model has helped to build the trade-off between economic gross margin maximization and the environmental objective of reducing water consumption. This point of compromise corresponds to the water demand curve at an optimal price (240 DT / 1000 m³). Applying this price leads to a slight decline in farm income and a significant gain in water saving. Price policy is necessary, but it is still an insufficient instrument, it can create a specialization in agricultural production for the most profitable crops. This specialization can create a shortage of certain agricultural products on the local market and sometimes on the wholesale market, affecting an imbalance in the marketing chain and asymmetrical price transmission.

It’s the time for public decision makers to rethink regulatory tools and intervention and consultation approaches with farmers for the sustainable management of water resources. Today, water saving needs to invest and subsidize in new irrigation technologies (Automatic Irrigation, Smartphone applications, desalination of seawater and Precision Irrigation and Airborne Remote Sensing).

References

• Al Atiri R., 2009. Politique du pays en matière de gestion de l’eau. Journée nationale de l’économie d’eau. INAT, 22 Mars, Tunis.
• Arabiyat S., 2005. Water price policies and incentives to reduce irrigation water demand: Jordan case study. In Lamaddalena N., Lebdi F., Todorovic M, Bogliotti C. (eds), Irrigation Systems performance. Bari: CIHEAM, 2005, 133-147 (Options Méditerranéennes: Série B. Etudes et Recherches; n. 52).
• Bachta M.S., Ben Mimoun A., Zaiebet L., Albouchi L., 2004. Simulation of a water market in Tunisia: case study of GIC Melalsa-Kairoun. Actes du Séminaire, Modernisation de l’agriculture irriguée, Rabat, Maroc, 19-23 Avril 2004.
• Ben Hamza E., 2017. Analyses de la viabilité socio-économique et environnementales des nouveaux systèmes de production. Mémoire (Master of Science), CIHEAM-IAMM, Montpellier, 176.
• Berbel J., Gomez-Limon J.A., 2000. The impact of water pricing policy in Spain: an analysis of three irrigated areas. Agricultural Water Management, 43: 219-238.
• Buysse J., Van Huylenbroeck G. and Lauwers L., 2007. Normative, positive and econometric mathematical programming as tools for incorporation of multi-functionality in agricultural policy modelling. Agriculture, Ecosystems and Environment, 120: 70-78.
• Chebil A., Frija A. and Thabet C., 2010. Irrigation water pricing between governmental policies and farmers’ perception: implications for green-houses horticultural production in Teboulba (Tunisia). Agricultural Economics Review, 11(2).
• Cohon J.L., Marks D.H., 1975. A Review and Evaluation of Multi-objective Programming Techniques. Water Resources Research, April 1975, 11(2): 208-220.
• De Fraiture C., Perry C., 2002. Why is the irrigation water demand curve inelastic at low price ranges? Paper presented at International conference on: Irrigation water Policies: Micro and macro considerations. Jointly organized by World Bank and Government of Morocco, Agadir, Morocco, June 15-17, 2002.
• El Chami D., Scardigno A., Zagnoli G., Malorgio G., 2011. Integrated irrigation water policies: economic and environmental impact in the “Renana” Reclamation and Irrigation Board, Italy. New Medit, 10(2): 25-32.
• Fragoso R. and Marques C., 2015. Alternative irrigation water pricing policies: An Econometric Mathematical Programming Model, New Medit, 14(4): 42-49.
• Golan A., Judge G. and Miller D., 1996. Maximum Entropy Econometrics. Chichester UK: Wiley.
• Heckelei T., Wolff H., 2003. Estimation of constrained optimization models for agricultural supply analysis based on generalized maximum entropy. European Review of Agricultural Economics, 30: 27-50.
• Howitt R.E., 1995. A calibration method for agricultural economic production models. American Journal of Agricultural Economics, 77(2): 329-342.
• Jeder H., Ben Khalifa A., Sghaier M., 2014. Economic analysis of water demand in publics irrigation systems in Tunisia, using FSSIM model. New Medit, 13(4): 46-53.
• Louhichi K., 2001. Essai de modélisation bio-économique de la relation agriculture-environnement – le cas de l’érosion en Tunisie. Thèse de Doctorat en Sciences Economiques, Université de Montpellier I: 252.
• Louhichi K., Gomez y Paloma S., 2014. A farm household model for agri-food policy analysis in developing countries: Application to smallholder farmers in Sierra Leone. Food Policy, 45: 1-13.
• MARH, 2013. Ministère de l’agriculture et des Ressources hydriques. Rapports des périmètres irrigués en Tunisie. 1998-2013.
• Mimouni M., Zekri S. and Flichman G., 2000. Modelling the tradeoffs between farm income and the reduction of erosion and nitrate pollution, Annals of Operations Research, 94: 91-103.
• Riesgo L., Gomez-Limon J.A., 2006. Multi-criteria policy scenario analysis for public regulation of irrigated agricultural. Agricultural Systems, 91: 1-28.
• Romero C. and Rehman T., 1989. Multiple Criteria Analysis for Agricultural Decisions. Amsterdam: Elsevier.
• Sghair M., 1995. Tarification et allocation optimale de l’eau d’irrigation dans les systèmes de production de la région oasienne de Nefzaoua (sud de la Tunisie). Ph.D. Thesis, Gent University, Belgium.
• Singh P. and Jakhar M., 2018. An application of multi objective compromise programming techniques: a case study of South India (Andhra Pradesh, Karnataka). International Journal of Management, Technology and Engineering, 8(8): 294-304.
• Thabet C., 2003. Réforme de la politique des prix de l’eau d’irrigation en Tunisie: approche en équilibre général. Ph.D. Thesis, ENSA de Rennes, France.
• Varela-Ortega C., Sumpsi M.J., Garrido A., Blanco M. and Iglesias E., 1998. Water pricing policies, public decision making and farmers’ response: implications for water policy. Agricultural Economics, 19: 193-202.